题目内容
【题目】如图，在边长为8的正方形
中，
、
分别是边
、
上的动点，且
，
为
中点，
是边
上的一个动点，则
的最小值是（ ）
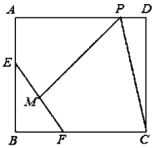
A.10B.
C.
D.
【答案】B
【解析】
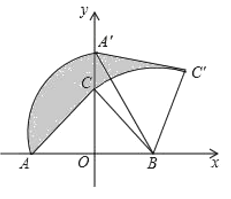
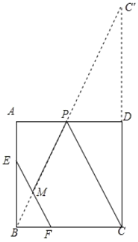
延长CD到C′，使C′D＝CD，CP＋PM＝C′P＋PM，当C′，P，N三点共线时，C′P＋PM的值最小，根据题意，点M的轨迹是以B为圆心，3为半径的圆弧上，圆外一点C′到圆上一点M距离的最小值C′M＝C′B3，根据勾股定理即可得到结论．
延长CD到C′，使C′D＝CD，
CP＋PM＝C′P＋PM，
当C′，P，M三点共线时，C′P＋PM的值最小，
根据题意，点M的轨迹是以B为圆心，3为半径的圆弧上，
圆外一点C′到圆上一点M距离的最小值C′M＝C′B3，
∵BC＝CD＝8，
∴CC′＝16，
∴C′B＝
，
∴CP＋PM的最小值是
3，
故选B．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某校计划购买一批学习笔记本，已知1本甲种笔记本和3本乙种笔记本共需26元；3本甲种笔记本和2本乙种笔记本共需29元．
（1）求购买一本甲种笔记本和一本乙种笔记本各需多少元；
（2）学校计划购进这两种笔记本共70本，并且甲种笔记本的数量不超过乙种笔记本数量的2倍，若设学校计划购进甲种比价本x本．
①填写下表：
甲种笔记本数量 | 10 |
|
乙种笔记本数量 |
| 30 |
所需总费用 |
|
|
②写出购买这两种笔记本所需要费用y（元）关于x的函数关系式；请设计出最省钱的购买方案，并说明理由
