Question

【题目】如图，已知AB为⊙O的直径，C为⊙O上一点，BG与⊙O相切于点B，交AC的延长线于点D（点D在线段BG上），AC = 8，tan∠BDC =

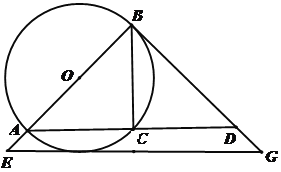
（1）求⊙O的直径；

（2）当DG=时，过G作，交BA的延长线于点E，说明EG与⊙O相切．

Answer 1

【答案】（1）10；（2）详见解析

【解析】

（1）先根据圆周角定理、圆的切线的性质得出，，再根据角互余的定义得出，然后根据正切的定义可求出BC的长，最后利用勾股定理即可得；

（2）如图（见解析），先根据平行线的性质得出，，，再根据中位线的判定与性质得出，然后根据正切的定义、勾股定理求出的长，从而可得MH的长，最后根据线段的和差求出为圆O的半径，根据圆的切线的判定即可得证．

（1）是圆O的直径

是圆O的切线

，即

在中，，即

解得

即圆O的直径为10；

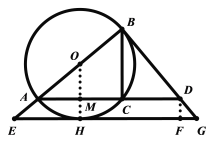
（2）如图，过点D作于F, 过点O作于H，交AD于M

，，

由（1）可知，，即

点O为AB的中点

是的中位线

在中，，即

设，则，

又

解得

，即OH为圆O的半径

EG与圆O相切．