题目内容
已知△ABC中,∠A=x°
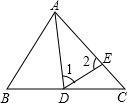
(1)如图1,若∠ABC和∠ACB的角平分线相交于点O,则用x表示∠BOC=______°
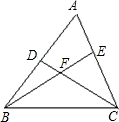
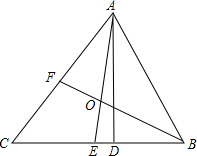
(2)如图2,若∠ABC和∠ACB的三等分线相交于点O1、O2,则用x表示∠BO1C=______°
(3)如图3,若∠ABC和∠ACB的n等分线相交于点O1、O2、…、On-1,则用x表示∠BO1C=______°

(1)如图1,若∠ABC和∠ACB的角平分线相交于点O,则用x表示∠BOC=______°
(2)如图2,若∠ABC和∠ACB的三等分线相交于点O1、O2,则用x表示∠BO1C=______°
(3)如图3,若∠ABC和∠ACB的n等分线相交于点O1、O2、…、On-1,则用x表示∠BO1C=______°

(1)∵∠ABC和∠ACB的角平分线相交于点O,
∴2∠OBC=∠ABC,2∠OCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠OBC+2∠OCB=180°,
∴∠OBC+∠OCB=90°-
∠A,
∵∠BOC=180°-(∠OBC+∠OCB)=90°+
∠A,
∵∠A=x°,
∴∠BOC=(90+
x)°;
(2)∵∠ABC和∠ACB的三等分线相交于点O1、O2,
∴∠O1BC=
∠ABC,∠O1CB=
∠ACB,
∴
∠O1BC=∠ABC,
∠O1CB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+
∠O1BC+
∠O1CB=180°,
∴∠O1BC+∠O1CB=
(180°-∠A),
∵∠BOC=180°-(∠O1BC+∠O1CB)=60°+
∠A,
∵∠A=x°,
∴∠BOC=(60+
x)°;
(3)由(1)(2)可得规律为:
若∠ABC和∠ACB的n等分线相交于点O1、O2、…、On-1,
则用x表示∠BO1C=(
+
x)°.
故答案为:(1)90+
x,(2)60+
x,(3)
+
x.
∴2∠OBC=∠ABC,2∠OCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠OBC+2∠OCB=180°,
∴∠OBC+∠OCB=90°-
| 1 |
| 2 |
∵∠BOC=180°-(∠OBC+∠OCB)=90°+
| 1 |
| 2 |
∵∠A=x°,
∴∠BOC=(90+
| 1 |
| 2 |
(2)∵∠ABC和∠ACB的三等分线相交于点O1、O2,
∴∠O1BC=
| 2 |
| 3 |
| 2 |
| 3 |
∴
| 3 |
| 2 |
| 3 |
| 2 |
∵∠A+∠ABC+∠ACB=180°,
∴∠A+
| 3 |
| 2 |
| 3 |
| 2 |
∴∠O1BC+∠O1CB=
| 2 |
| 3 |
∵∠BOC=180°-(∠O1BC+∠O1CB)=60°+
| 2 |
| 3 |
∵∠A=x°,
∴∠BOC=(60+
| 2 |
| 3 |
(3)由(1)(2)可得规律为:
若∠ABC和∠ACB的n等分线相交于点O1、O2、…、On-1,
则用x表示∠BO1C=(
| 180 |
| n |
| n-1 |
| n |
故答案为:(1)90+
| 1 |
| 2 |
| 2 |
| 3 |
| 180 |
| n |
| n-1 |
| n |

练习册系列答案
相关题目