题目内容
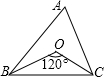
如图△ABC中，∠B=42°，∠DAE=14°，AD、AE分别是△ABC的高和角平分线．求：∠C的度数．
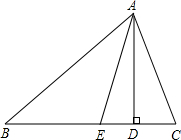
设∠C=x，
∵AD⊥BC，∴∠CAD=90°-x，
则∠EAC=∠DAE+∠CAD=104°-x，
又∵AE分别是△ABC的角平分线，∴∠BAC=2∠EAC，
在△ABC中，∵∠B+∠C+∠BAC=180°，
∴42°+x+2（104°-x）=180°，
解得x=70，即∠C=70°．
∵AD⊥BC，∴∠CAD=90°-x，
则∠EAC=∠DAE+∠CAD=104°-x，
又∵AE分别是△ABC的角平分线，∴∠BAC=2∠EAC，
在△ABC中，∵∠B+∠C+∠BAC=180°，
∴42°+x+2（104°-x）=180°，
解得x=70，即∠C=70°．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
