Question

【题目】等边三角形的边长为，将其放置在如图所示的平面直角坐标系中，其中边在轴上，边的高在轴上．一只电子虫从出发，先沿轴到达点，再沿到达点，已知电子虫在轴上运动的速度是在上运动速度的倍，若电子虫走完全程的时间最短，则点的坐标为________．

Answer 1

【答案】

【解析】

如图作GM⊥AB于M，设电子虫在CG上的速度为v，电子虫走完全全程的时间t=，在Rt△AMG中，GM=AG，TC 电子虫走完全全程的时间t=（GM+CG），当C、G、M共线时，且CM⊥AB时，GM+CG最短，由此即可解决问题．

如图作GM⊥AB于M，

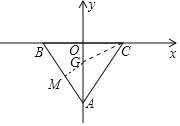
设电子虫在CG上的速度为v，

电子虫走完全全程的时间t=，

在Rt△AMG中，GM=AG，

∴电子虫走完全全程的时间t=（GM+CG），

当C、G、M共线时，且CM⊥AB时，GM+CG最短，

此时CG=AG=2OG，易知OG=×6=，

所以点G的坐标为（0，-）．
故答案为：（0，-）．