��Ŀ����
����Ŀ�����һ���������ܱ�һ���߶ηָ���������������Σ���ô�������߶�Ϊ��������ε������ߣ������������Ϊ���������Σ�
��1����ͼ1����ABC�ǵ�����������Σ�AB=AC(![]() )������ABC�Ľ�ƽ����BD��AC�ڵ�D����BD����ABC��һ�������ߣ�����BDC=______�ȣ�
)������ABC�Ľ�ƽ����BD��AC�ڵ�D����BD����ABC��һ�������ߣ�����BDC=______�ȣ�
��2����ͼ2����ABC�У���B=2��C���߶�AC�Ĵ�ֱƽ���߽�AC�ڵ�D����BC�ڵ�E����֤��AE����ABC��һ�������ߣ�
��3����ͼ3����֪��ABC�����������Σ�����A=30������BΪ�۽ǣ�������п��ܵ���B�Ķ�����������Ҫ�����ڴ����Ӧλ�����⻭ͼ����

���𰸡���1��72�� ��2��֤������������3��135���112.5���140�㣮
�������������������1��ֻҪ֤����ABE����AEC�ǵ��������μ��ɣ���2����ͼ2�У���BD��������ʱ���������������ۣ���ͼ3�У���AD��������ʱ��AB=BD��AD=DC���ݵ������������ʼ��ɽ�����⣬��CDΪ������ʱ���������⣮
�����������1��֤������ͼ1�У�
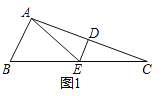
��DE���߶�AC�Ĵ�ֱƽ���ߣ�
��EA=EC������EAC�ǵ���������
���EAC=��C��
���AEB=��EAC+��C=2��C��
�ߡ�B=2��C��
���AEB=��B������EAB�ǵ��������Σ�
��AE����ABC��һ�������ߣ�
��2����ͼ2����

��BD��������ʱ�����AB=BD=DC������ABC=��ABD+��DBC=120��=15��=135����
���AD=AB��DB=DC������ABC=��ABD+��DBC=75��+37.5��=112.5����
���AD=DB��DC=CB������ABC=��ABD+��DBC=30��+60��=90��������������������
��ͼ3�У���AD��������ʱ��AB=BD��AD=DC������ABC=180��-20��-20��=140��
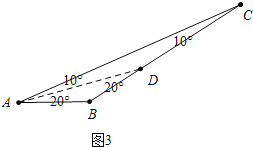
��CDΪ������ʱ���������⣮
��������������ABC�Ķ���Ϊ135����112.5����140����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�






