题目内容
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=![]() 的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为( )
的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为( )

A. 5 B. 6 C. 4![]() D. 5
D. 5![]()
【答案】D
【解析】
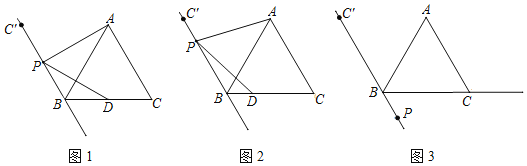
过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,根据直线AB的解析式为y=![]() x+2,可得PF=
x+2,可得PF=![]() ,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+
,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+![]() ,FD=1+2-x=3-x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程(
,FD=1+2-x=3-x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程(![]() )2+(3-x)2=(x+
)2+(3-x)2=(x+![]() )2,解方程求得x=1,即可得D(1,0),再直线AD的解析式为y=3x-3,最后解方程组
)2,解方程求得x=1,即可得D(1,0),再直线AD的解析式为y=3x-3,最后解方程组 求得C点坐标.解方程组
求得C点坐标.解方程组 求得点M的坐标,再根据两点间的距离公式即可求得CM的长.
求得点M的坐标,再根据两点间的距离公式即可求得CM的长.
如图所示,过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,

根据点A(2,3)和点B(0,2),可得直线AB的解析式为y=![]() x+2,点A在反比例函数y=
x+2,点A在反比例函数y=![]() 的图象上,可得y=
的图象上,可得y=![]() ,
,
由A(2,3),可得OF=1,
当x=-1时,y=-![]() +2=
+2=![]() ,即P(-1,
,即P(-1,![]() ),
),
∴PF=![]() ,
,
将△AGP绕点A逆时针旋转90°得△AEH,则△ADP≌△ADH,
∴PD=HD,PG=EH=![]() ,
,
设DE=x,则DH=DP=x+![]() ,FD=1+2-x=3-x,
,FD=1+2-x=3-x,
Rt△PDF中,PF2+DF2=PD2,
即(![]() )2+(3-x)2=(x+
)2+(3-x)2=(x+![]() )2,
)2,
解得x=1,
∴OD=2-1=1,即D(1,0),
根据点A(2,3)和点D(1,0),可得直线AD的解析式为y=3x-3,
解方程组 可得
可得![]() 或
或![]()
∴C(-1,-6),
解方程组 可得
可得![]() 或
或![]()
∴M(-6,-1),
∴![]() .
.
故选D.

练习册系列答案
相关题目