题目内容
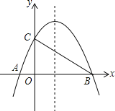
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .若已知
.若已知![]() 点的坐标为
点的坐标为![]() .点
.点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标为________.
的坐标为________.
【答案】![]() ,
,![]() ,
,![]()
【解析】
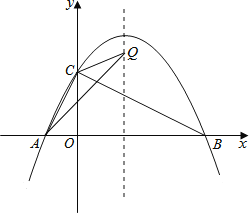
首先求出抛物线解析式,然后利用配方法或利用公式x=-![]() 求出对称轴方程,由此可设可设点Q(3,t),若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.
求出对称轴方程,由此可设可设点Q(3,t),若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.
∵抛物线y=-![]() x2+bx+4的图象经过点A(-2,0),
x2+bx+4的图象经过点A(-2,0),
∴-![]() ×(-2)2+b×(-2)+4=0,
×(-2)2+b×(-2)+4=0,
解得:b=![]() ,
,
∴抛物线解析式为 y=-![]() x2+
x2+![]() x+4,
x+4,
又∵y=-![]() x2+
x2+![]() x+4=-
x+4=-![]() (x-3)2+
(x-3)2+![]() ,
,
∴对称轴方程为:x=3,
∴可设点Q(3,t),则可求得:
AC=![]() ,
,
AQ=![]() ,
,
CQ=![]() .
.
i)当AQ=CQ时,
有![]() =
=![]() ,
,
即25+t2=t2-8t+16+9,
解得t=0,
∴Q1(3,0);
ii)当AC=AQ时,
有![]() =2
=2![]() ,
,
即t2=-5,此方程无实数根,
∴此时△ACQ不能构成等腰三角形;
iii)当AC=CQ时,
有2![]() =
=![]() ,
,
整理得:t2-8t+5=0,
解得:t=4±![]() ,
,
∴点Q坐标为:Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).
综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).
故答案为:(3,0),(3,4+![]() ),(3,4-
),(3,4-![]() ).
).

练习册系列答案
相关题目