题目内容
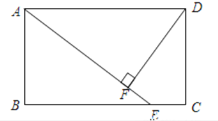
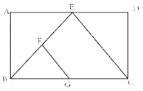
【题目】如图，在矩形ABCD，BE平分
，交AD于点E，F是BE的中点，G是BC的中点，连按EC，若
，
，则FG的长为________。
【答案】5
【解析】
根据BE平分∠ABC，可得∠ABE=45°，△ABE是等腰直角三角形，再根据勾股定理可得EC，根据F是BE的中点，G是BC的中点，可判定FG是△BEC的中位线，即可求得FG=
EC .
∵矩形ABCD中，BE平分∠ABC，
∴∠A=90°，∠ABE=45°，
∴ABE是等腰直角三角形，
∴AE=AB
又∵ABCD是矩形，
∴AB=BC=14， DC=AB=8，∠EDC=90°，
∴DE=AD-AE=14-8=6，
EC=
，
∵F是BE的中点，G是BC的中点，
∴FG=EC=5 .
故答案为5 .
练习册系列答案
相关题目
