题目内容
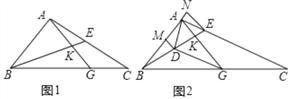
【题目】如图1,已知△ABC中,∠ABC=45°,点E为AC上的一点,连接BE,在BC上找一点G,使得AG=AB,AG交BE于K.
(1)若∠ABE=30°,且∠EBC=∠GAC,BK=4,求AC的长度.
(2)如图2,过点A作DA⊥AE交BE于点D,过D、E分别向AB所在的直线作垂线,垂足分别为点M、N,且NE=AM,若D为BE的中点,证明: ![]() DG=2AG.
DG=2AG.
【答案】(1)AC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)如图1中,作AH⊥BG于H.在Rt△ABK中,求出AK、AB.在Rt△ABH中,求出AH.在Rt△AHC中,证明∠C=30°,即可推出AC=2AH,由此解决问题.
(2)如图2中,连接EG.由△MAD≌△NEA,推出AD=AE再证明△BAD≌△GAE,推出BD=EG=DE,∠ABD=∠AGE,推出DGE是等腰直角三角形,设AD=AE=a,求出DG、AG即可解决问题.
试题解析:解:(1)如图1中,作AH⊥BG于H.
在Rt△ABK中,∵∠BAK=90°,∠ABK=30°,BK=4,∴AK=![]() BK=2,AB=
BK=2,AB=![]() =
=![]() .∵AB=AG,∠BAC=90°,∴∠ABC=∠AGB=45°,∠CBE=∠CAG=15°.∵∠AGB=∠C+∠CAG,∴∠C=30°.在Rt△AHC中,∵∠AHC=90°,∠C=30°,∴AC=2AH.在Rt△ABH中,AH=BH=
.∵AB=AG,∠BAC=90°,∴∠ABC=∠AGB=45°,∠CBE=∠CAG=15°.∵∠AGB=∠C+∠CAG,∴∠C=30°.在Rt△AHC中,∵∠AHC=90°,∠C=30°,∴AC=2AH.在Rt△ABH中,AH=BH=![]() AB=
AB=![]() ,∴AC=
,∴AC=![]() .
.

(2)如图2中,连接EG.∵DM⊥AB,EN⊥BA,∴∠AMD=∠N=∠DAE=90°,∴∠MAD+∠NAE=90°,∠NAE+∠NEA=90°,∴∠MAD=∠NEA.
在△MAD和△NEA中,∵∠MAD=∠AEN,AM=NE,∠AMD=∠NEA,∴△MAD≌△NEA,∴AD=AE.∵∠BAC=∠DAE=90°,∴∠BAD=∠GAE.
在△BAD和△GAE中,∵BA=AG,∠BAD=∠GAE,AD=AE,∴△BAD≌△GAE,∴BD=EG=DE,∠ABD=∠AGE.∵∠AKB=∠EKG,∴∠KEG=∠KAB=90°,∴△DGE是等腰直角三角形.设AD=AE=a,∴∠ADE=∠EDG=45°,∴∠ADG=90°,∴DE=BD=EG=![]() a,DG=
a,DG=![]() DE=2a.
DE=2a.
在Rt△ADG中,AG=![]() =
= ![]() ,∴
,∴![]() ,∴
,∴![]() DG=2AG.
DG=2AG.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案