题目内容
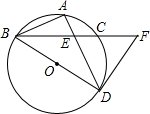 已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB.
已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB.(1)求证:AB2=AE•AD;
(2)过点D作⊙O的切线,与BC的延长线交于点F,若AE=2,ED=4,求EF的长.
分析:(1)点A是劣弧BC的中点,即可得∠ABC=∠ADB,又由∠BAD=∠EAB,即可证得△ABE∽△ADB,根据相似三角形的对应边成比例,即可证得AB2=AE•AD;
(2)由(1)求得AB的长,又由BD为⊙O的直径,即可得∠A=90°,由DF是⊙O的切线,可得∠BDF=90°,在Rt△ABD中,求得tan∠ADB的值,即可求得∠ADB的度数,即可证得△DEF是等边三角形,则问题得解.
(2)由(1)求得AB的长,又由BD为⊙O的直径,即可得∠A=90°,由DF是⊙O的切线,可得∠BDF=90°,在Rt△ABD中,求得tan∠ADB的值,即可求得∠ADB的度数,即可证得△DEF是等边三角形,则问题得解.
解答:解:(1)证明:∵点A是劣弧BC的中点,
∴∠ABC=∠ADB.(1分)
又∵∠BAD=∠EAB,
∴△ABE∽△ADB.(2分)
∴
=
.
∴AB2=AE•AD.(3分)
(2)解:∵AE=2,ED=4,
∵△ABE∽△ADB,
∴
=
,
∴AB2=AE•AD,
∴AB2=AE•AD=AE(AE+ED)=2×6=12.
∴AB=2
(舍负).(4分)
∵BD为⊙O的直径,
∴∠A=90°.
又∵DF是⊙O的切线,
∴DF⊥BD.
∴∠BDF=90°.
在Rt△ABD中,tan∠ADB=
=
=
,
∴∠ADB=30°.
∴∠ABC=∠ADB=30°.
∴∠DEF=∠AEB=60°,∠EDF=∠BDF-∠ADB=90°-30°=60°.
∴∠F=180°-∠DEF-∠EDF=60°.
∴△DEF是等边三角形.
∴EF=DE=4.(5分)
∴∠ABC=∠ADB.(1分)
又∵∠BAD=∠EAB,
∴△ABE∽△ADB.(2分)
∴
| AB |
| AE |
| AD |
| AB |
∴AB2=AE•AD.(3分)
(2)解:∵AE=2,ED=4,
∵△ABE∽△ADB,
∴
| AB |
| AE |
| AD |
| AB |
∴AB2=AE•AD,
∴AB2=AE•AD=AE(AE+ED)=2×6=12.
∴AB=2
| 3 |
∵BD为⊙O的直径,
∴∠A=90°.
又∵DF是⊙O的切线,
∴DF⊥BD.
∴∠BDF=90°.
在Rt△ABD中,tan∠ADB=
| AB |
| AD |
2
| ||
| 6 |
| ||
| 3 |
∴∠ADB=30°.
∴∠ABC=∠ADB=30°.
∴∠DEF=∠AEB=60°,∠EDF=∠BDF-∠ADB=90°-30°=60°.
∴∠F=180°-∠DEF-∠EDF=60°.
∴△DEF是等边三角形.
∴EF=DE=4.(5分)
点评:此题考查了相似三角形的判定与性质,圆的切线的性质,以及三角函数等知识.此题综合性较强,难度适中,解题的关键是数形结合思想的应用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 点E,AE=2,ED=4.
点E,AE=2,ED=4. 已知:如图,BD为ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.求证:DE=DF.
已知:如图,BD为ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.求证:DE=DF. 23、已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.
23、已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F. 已知,如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.试判断四边形BFDE的形状,并证明你的结论.
已知,如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.试判断四边形BFDE的形状,并证明你的结论.