题目内容
已知：如图，BD为ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F．求证：DE=DF．
分析：可通过证明OE=OF，然后根据垂直平分线性质来得出DE=DF，要证明OE=OF，证明三角形BOF和三角形DOE全等即可．
解答：证明：在平行四边形ABCD中，AD∥BC，
∴∠OBF=∠ODE
∵O为BD的中点
∴OB=OD
在△BOF和△DOE中，
∵
∴△BOF≌△DOE
∴OF=OE
∵EF⊥BD于点O
∴DE=DF．
∴∠OBF=∠ODE
∵O为BD的中点
∴OB=OD
在△BOF和△DOE中，
∵
|
∴△BOF≌△DOE
∴OF=OE
∵EF⊥BD于点O
∴DE=DF．
点评：本题考查了平行四边形的性质，垂直平分线的性质，全等三角形的判定等知识点，证明简单的线段相等，一般是通过全等三角形来证明的．
练习册系列答案
相关题目
点E，AE=2，ED=4．
23、已知：如图，BD为平行四边形ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD，BC分别交于点E，F．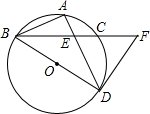
已知：如图，BD为⊙O的直径，点A是劣弧BC的中点，AD交BC于点E，连接AB．
已知，如图，BD为平行四边形ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F．试判断四边形BFDE的形状，并证明你的结论．