题目内容
 23、已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.
23、已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD,BC分别交于点E,F.求证:
(1)△BOF≌△DOE.
(2)DE=DF.
分析:(1)根据平行四边形的性质得到AD∥BC,推出∠ADB=∠DBC,根据三角形全等的判定即可推出结论;
(2)先证四边形BEDF是平行四边形,根据EF⊥BD,得出菱形BEDF,根据菱形的性质即可得出答案.
(2)先证四边形BEDF是平行四边形,根据EF⊥BD,得出菱形BEDF,根据菱形的性质即可得出答案.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵∠DOE=∠BOF,OB=OD,
∴△BOF≌△DOE.
(2)证明:连接BE,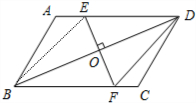
∵△BOF≌△DOE,
∴DE=BF,
∵DE‖BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD
∴平行四边形BEDF为菱形,
∴DE=DF.
∴AD∥BC,
∴∠ADB=∠DBC,
∵∠DOE=∠BOF,OB=OD,
∴△BOF≌△DOE.
(2)证明:连接BE,

∵△BOF≌△DOE,
∴DE=BF,
∵DE‖BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD
∴平行四边形BEDF为菱形,
∴DE=DF.
点评:本题主要考查对平行四边形的性质和判定,平行线的性质,菱形的性质和判定,全等三角形的性质和判定等知识点的理解和掌握,能灵活运用这些性质进行证明是证此题的关键,题型较好,难度适中.

练习册系列答案
相关题目

 ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
 的大小关系.
的大小关系.
 ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
 的大小关系.
的大小关系.
 ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
 的大小关系.
的大小关系.
 ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
 的大小关系.
的大小关系.