题目内容
已知：如图，BD为⊙O的直径，BC为弦，A为BC弧中点，AF∥BC交DB的延长线于点F，AD交BC于
点E，AE=2，ED=4．（1）求证：AF是⊙O的切线；
（2）求AB的长．
分析：（1）连接AO，证明AO⊥AF由切线的判定定理可以得出AF是⊙O的切线．
（2）先根据相似三角形的判定得到△ABE∽△ADB，从而根据相似三角形的对应边成比例即可得到AD的长．
（2）先根据相似三角形的判定得到△ABE∽△ADB，从而根据相似三角形的对应边成比例即可得到AD的长．
解答：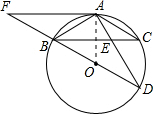
（1）证明：连接OA，
∵A是BC弧的中点，
∴OA⊥BC．
∵AF∥BC，
∴OA⊥AF．
∴AF是⊙O的切线．
（2）解：∵∠BAE=DAB，∠ABE=∠ADB，
∴△ABE∽△ADB．
∴
=
．
∴AB2=AE•AD=12．
∴AB=2
．
（1）证明：连接OA，∵A是BC弧的中点，
∴OA⊥BC．
∵AF∥BC，
∴OA⊥AF．
∴AF是⊙O的切线．
（2）解：∵∠BAE=DAB，∠ABE=∠ADB，
∴△ABE∽△ADB．
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AE•AD=12．
∴AB=2
| 3 |
点评：此题主要考查切线的判定，平行线的性质及圆周角定理等知识点的综合运用．
练习册系列答案
相关题目
已知：如图，BD为ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F．求证：DE=DF．
23、已知：如图，BD为平行四边形ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD，BC分别交于点E，F．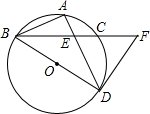
已知：如图，BD为⊙O的直径，点A是劣弧BC的中点，AD交BC于点E，连接AB．
已知，如图，BD为平行四边形ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F．试判断四边形BFDE的形状，并证明你的结论．