Question

【题目】如图，正方形的边长为4，点是的中点，平分交于点，将绕点顺时针旋转90°得，则的长为_____．

Answer 1

【答案】

【解析】

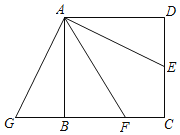
作 ，如图，易得四边形CFMD为矩形，则，利用勾股定理计算出 ，再根据旋转的性质得到，于是可判断点G在CB的延长线上，接着证明FA平分∠GAD得到FN＝FM＝4，然后利用面积法计算出GF，从而计算CG﹣GF就可得到CF的长．

解：

作 ，如图，易得四边形CFMD为矩形，则∵正方形ABCD的边长为4，点是的中点，

∴

∵△ADE绕点A顺时针旋转90°得△ABG，

∴

而 ，

∴点G在CB的延长线上，

∵AF平分∠BAE交BC于点F，

∴∠1＝∠2，

∴∠2+∠4＝∠1+∠3，即FA平分∠GAD，

∴FN＝FM＝4，

∵,

∴,

∴ ．

故答案为．