题目内容
【题目】正方形ABCD的边长为3,如图将正方形ABCD点沿对角线BD折叠使点C与点A重合,在BD上取一点E,过E作EF⊥AD于F.继续将△EFD沿EF折叠使D与AF上点M重合,M恰好为AF的中点,设BE的中点为P,连接PF,则PF的长为__________.
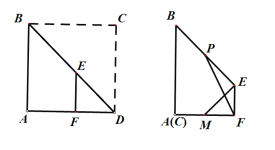
【答案】![]()
【解析】
将△EFD沿EF折叠使D与AF上点M重合,则FD=MF.M恰好为AF的中点,故AM=MF=FD=1,
由于EF⊥AD,则FE∥AB,则∠FED=∠BAD=45°,故可知△EFD为直角等腰直角三角形,则EF=FD=1,连接PM,由FE∥AB,则知四边形BAFE为梯形.在梯形BAFE中,P、M分别为BE、AF的中点,根据中位线定理可知PM![]() AF,在Rt△PMF中根据勾股定理即课求得PF的大小.
AF,在Rt△PMF中根据勾股定理即课求得PF的大小.
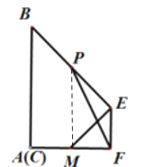
将△EFD沿EF折叠使D与AF上点M重合,
则FD=MF.
M恰好为AF的中点,正方形边长为3,
则AM=MF=FD=1.
EF⊥AD,BA⊥AD,
则FE∥AB.
∠FED=∠BDA=45°=∠FDE,
故△EFD为直角等腰直角三角形,
则EF=FD=1,
连接PM,在梯形BAFE中,P、M分别为BE、AF的中点,
根据中位线定理可知PM∥BA,故PM![]() AF,且PM=
AF,且PM=![]() =
=![]() =2.
=2.
在Rt△PMF中,PM=2,MF=1,
![]() =
=![]() +
+![]() ,
,
故PF=![]() =
=![]() .
.

练习册系列答案
相关题目