题目内容
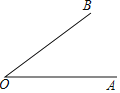
【题目】如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE上AD,交BD的延长线于点E.
(1)求证:∠E=![]() ∠C;
∠C;
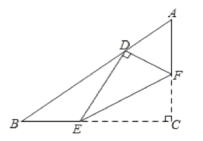
(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数,并直接写出![]() 的值.
的值.

【答案】(1)见解析;(2)cos∠ABC的值为2∶3;(3)∠ABC=30°或∠ABC=45°,![]() 的值
的值![]() 或
或![]()
【解析】
(1)由AE⊥AD,得到∠DAE=90°,∠E=90°-∠ADE,再由AD平分∠BAC,得到∠ABD![]() ∠BAC,即可解答
∠BAC,即可解答
(2)延长AD交BC于点F,得出![]() ,再利用三角函数即可即可
,再利用三角函数即可即可
(3)根据题意得出∠ABC=∠E=![]() ∠C,继而可得∠ABC=30°,
∠C,继而可得∠ABC=30°,![]() ,∠ABC=45°,
,∠ABC=45°,![]() ,即可解答
,即可解答
证明:∵AE⊥AD,
∴∠DAE=90°,∠E=90°-∠ADE.
∵AD平分∠BAC,∴∠BAD![]() ∠BAC,同理∠ABD
∠BAC,同理∠ABD![]() ∠BAC
∠BAC
又∵∠ADE=∠BAD+∠ABD,∠BAC+∠ABC=180°-∠C,
∴∠ADE![]() (∠BAC+∠BAC)
(∠BAC+∠BAC)![]() (180°-∠C).
(180°-∠C).
∴∠E=90°-![]() (180°-∠C)
(180°-∠C)![]() ∠C
∠C
解:延长AD交BC于点F.
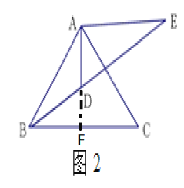
∵AE=AB,∴∠ABE=∠E.
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠CBE=∠E.
∴AE∥ BC.
∴∠AFB=∠FAE=90°,![]()
又∵BD∶DE=2∶3
∴cos∠ABC=![]()
∴cos∠ABC的值为2∶3.
(3)解:△ABC与△ADE相似,且∠DAE=90°,
∴△ABC中必有一个内角等于90°.
∵ABC是锐角,
∴∠ABC≠90°.
若∠BAC=∠DAE=90°,
∵∠E=![]() ∠C,∴∠ABC=∠E=
∠C,∴∠ABC=∠E=![]() ∠C
∠C
∵∠ABC+∠C=90°,∴∠ABC=30°.这时![]()
综上所述,∠ABC=30°或∠ABC=45°,![]() 的值
的值![]() 或
或![]()

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案