题目内容
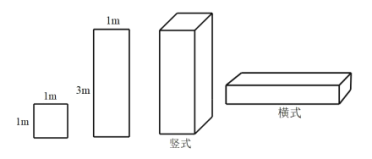
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
【答案】(1)最多制作竖式箱子5个;(2)45、34、23、12.
【解析】
(1)根据题意可以列出相应的不等式,从而可以求得最多可以制作竖式箱子多少个;
(2)根据题意可以列出相应的二元一次方程,再根据a为整数和a≥10,即可解答本题.
解:(1)由题意可得,
1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,
设竖式箱子x个,则横式箱子(10-x)个,
(20+4×60)x+(2×20+3×60)(10-x)≤2400,
解得,x≤5,
∴x的最大值是5,
答:最多可以制作竖式箱子5个;
(2)如图

C型可以看成三列,每一列可以做成3个A型或1个B型,65个C型就有65×3=195列,
∵材料恰好用完,
∴最后A型的数量一定是3的倍数,
设竖式a个,横式b个,
∵1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,1个B型相当于3个A型,
∴(1+4×3)a+(2+3×3)b=195×3,
∴13a+11b=585,
∵![]() 和
和![]() 都是整数,且
都是整数,且![]() ,
,
解得:![]() 、
、![]() 、
、![]() 、
、![]() ,
,
经验证,四种情况下![]() 型板数量均为3的倍数,
型板数量均为3的倍数,
故答案为:45、34、23、12.

练习册系列答案
相关题目