题目内容
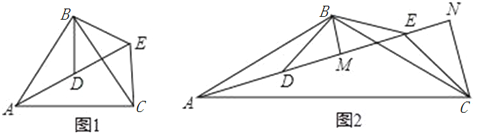
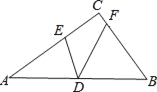
【题目】如图，在△ABC中，∠ACB=90°，D为边AB的中点，E，F分别为边AC，BC上的点，且AE=AD，BF=BD．若DE=2
，DF=4，则AB的长为_____．
【答案】4
【解析】如图，延长FD到M使得DM=DF，连接AM、EM、EF，作EN⊥DF于N．∵AE=AD，BF=BD，∴∠AED=∠ADE，∠BDF=∠BFD，∴2∠ADE+∠BAC=180°，2∠BDF+∠B=180°，∴2∠ADE+2∠BDF=270°，∴∠ADE+∠BDF=135°，∴∠EDF=180°﹣（∠ADE+∠BDF）=45°，∵∠END=90°，DE=2
，∴∠EDN=∠DEN=45°，∴EN=DN=2，在△DAM和△DBF中，DA=DB，∠ADM=∠BDF，DM=DF，∴△ADM≌△BDF，∴BF=AM=BD=AD=AE，∠MAD=∠B，∴∠MAE=∠MAD+∠BAC=90°，∴EM=
AM，在RT△EMN中，∵EN=2，MN=DM+DN=6，∴EM=
=2
，∴AM=2
，AB=2AM=4
，故答案为4
．
练习册系列答案
相关题目
【题目】求一个正数的算术平方根，有些数可以直接求得，如
，有些数则不能直接求得，如
，但可以通过计算器求得，还可以通过一组数的内在联系，运用规律求得.请同学们观察下表：
| 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表述出来）
（2）运用你发现的规律，探究下列问题：已知
，求下列各数的算术平方根：
①0.0206；②2060000.
