Question

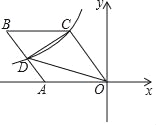
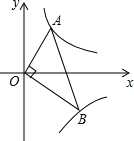
【题目】如图，已知点A、B分别在反比例函数y＝（x＞0），y＝﹣（x＞0）的图象上，且OA⊥OB，则的值为_____．

Answer 1

【答案】．

【解析】

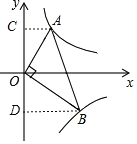
作AC⊥y轴于C，BD⊥y轴于D，如图，利用反比例函数图象上点的坐标特征和三角形面积公式得到S△OAC＝，S△OBD＝，再证明Rt△AOC∽Rt△OBD，然后利用相似三角形的性质得到的值．

解：作AC⊥y轴于C，BD⊥y轴于D，如图，

∵点A、B分别在反比例函数y＝（x＞0），y＝﹣（x＞0）的图象上，

∴S△OAC＝×1＝，S△OBD＝×|﹣5|＝，

∵OA⊥OB，

∴∠AOB＝90°

∴∠AOC+∠BOD＝90°，

∴∠AOC＝∠DBO，

∴Rt△AOC∽Rt△OBD，

∴＝（）2＝＝，

∴＝．

∴＝．

故答案为：．