题目内容
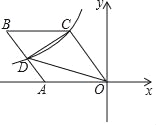
【题目】如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=
，反比例函数y=﹣
的图象经过点C，与AB交与点D，则△COD的面积的值等于_____；
【答案】10．
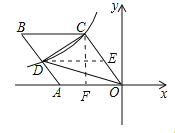
【解析】分析：易证S菱形ABCO=2S△CDO，再根据tan∠AOC的值，可以假设OF=3x，推出OC=5x，可得OA=OC=5x，S菱形ABCO=AOCF=20x2，由C（﹣3x，4x），可得
×3x×4x=6，推出x2=1，由此即可解决问题．
详解：作DE∥AO，CF⊥AO，设CF=4x，
∵四边形OABC为菱形，∴AB∥CO，AO∥BC．
∵DE∥AO，∴S△ADO=S△DEO，同理S△BCD=S△CDE．
∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE，∴S菱形ABCO=2（S△DEO+S△CDE）=2S△CDO．
∵tan∠AOC=
，∴OF=3x，∴OC=5x，∴OA=OC=5x．
∵S菱形ABCO=AOCF=20x2．
∵C（﹣3x，4x），∴×3x×4x=6，∴x2=1，∴S菱形ABCO=20，∴△COD的面积=10．
故答案为：10．
练习册系列答案
相关题目
