题目内容
如图，在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AC，则AE：EC=______．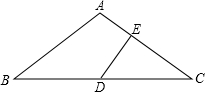
∵AB=AC，∠BAC=120°
∴∠ABC=∠ACB=30°
连接AD
∵DE⊥AC
∴∠AED=∠DEC=90°，∠ADE=30°（等腰三角形三线合一定理）
设AE=x，则AD=2x，AC=2AD=4x
∴EC=3x
即AE：EC=x：3x=1：3．
故填1：3．
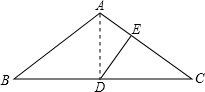
∴∠ABC=∠ACB=30°
连接AD
∵DE⊥AC
∴∠AED=∠DEC=90°，∠ADE=30°（等腰三角形三线合一定理）
设AE=x，则AD=2x，AC=2AD=4x
∴EC=3x
即AE：EC=x：3x=1：3．
故填1：3．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
