题目内容
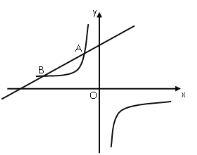
【题目】(1)写出图1中函数图象的解析式![]() ;
;

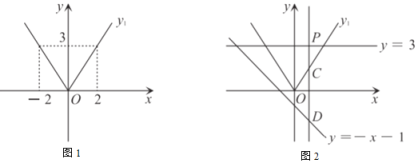
(2)如图2,过直线![]() 上一点
上一点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 的图象于点
的图象于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①试比较![]() 与
与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
②若![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() 或
或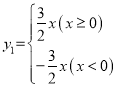 ;(2)①当
;(2)①当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,证明见解析;②
,证明见解析;②![]() 或
或![]() .
.
【解析】
(1)应用待定系数法,分类讨论求解析式;
(2)①观察点P的位置,可以发现随着点P的运动,点C的坐标表示发生变化,因而进行分类讨论求m范围即可;
②由图象可知,点C在点D上方,分别根据m>0和m≤0时的CD值分类讨论求m范围.
解:(1)如图:
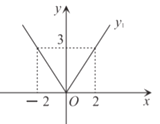
设![]() ,则
,则
当![]() 时,图像经过点(2,3),
时,图像经过点(2,3),
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ;
;
当![]() 时,图像经过点(-2,3),
时,图像经过点(-2,3),
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ;
;
∴函数的解析式为:![]() 或
或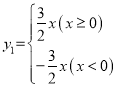 ;
;
故答案为:![]() 或
或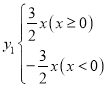 ;
;
![]() 由已知得,点C坐标为(m,
由已知得,点C坐标为(m,![]() m),点D坐标为(m,-m-1),则PD=3-(-m-1)=4+m,
m),点D坐标为(m,-m-1),则PD=3-(-m-1)=4+m,
当点C在直线y=3下方时或在直线y=3上时,由图象可知PC<PD,
当点C在直线y=3上方时,CP=![]() m-3,
m-3,
∴当CP=PD时,![]() m-3=4+m,
m-3=4+m,
解得:m=14,
当CP>PD时,![]() m-3>4+m,
m-3>4+m,
解得:m>14,
当CP<PD时,![]() m-3<4+m,
m-3<4+m,
解得:m<14
综上所述,当0<m<14时,CP<PD,当m=14时,CP=PD,当m>14时,CP>PD;
②当m>0时,点C坐标为(m,![]() m),点D坐标为(m,-m-1),
m),点D坐标为(m,-m-1),
∴![]() ,
,
![]() ,
,
![]() ;
;
当m≤0时,点C坐标为(m,![]() m),点D坐标为(m,-m-1),
m),点D坐标为(m,-m-1),
则CD=![]() m-(-m-1)=
m-(-m-1)=![]() m+1=3,
m+1=3,
解得:m=![]() ;
;
∴当![]() 时,
时,![]() 的值为
的值为![]() 或
或![]() ;
;

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目