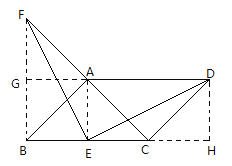
题目内容
【题目】如图,在平行四边形![]() 中,连接
中,连接![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .求证:
.求证:![]() .
.

【答案】证明步骤见解析
【解析】
连接BF,AE分别过点A,D向BF和BC的延长线作垂线,垂足是G,H,先证明四边形AEBG是正方形,再证明Rt△FBE≌Rt△EHD(HL),最后由全等的性质证明∠BEF+∠HED=90°即可解题.
解:连接BF,AE分别过点A,D向BF和BC的延长线作垂线,垂足是G,H
∵在平行四边形![]() 中,
中, ![]() ,且
,且![]()
∴△BAC和△ACD是等腰直角三角形,
∵![]() 是
是![]() 的中点,
的中点,
∴AE⊥BC,
∴AE=DH,四边形AEBG是正方形,
∴∠FBE=90°,BE=DH,
在Rt△FBE和Rt△EHD中
![]()
∴Rt△FBE≌Rt△EHD(HL)
∴∠BFE=∠HED,
∵∠BFE+∠BEF=90°
∴∠BEF+∠HED=90°,即∠FED=90°,
∴ED⊥EF

练习册系列答案
相关题目
【题目】某公司计划组织员工外出甲、乙旅行社的服务质量相问,且对外报价都是300元/人,该公司联系时,甲旅行社表示可给每人八折优惠;乙旅行社表示可免去一人的费用,其余人九折优惠.
(1)根据题意,填写下表:
外出人数(人) | 10 | 11 |
甲旅行社收费(元) | ____ | 2640 |
乙旅行社收费(元) | 2430 | ____ |
(2)设该公司此次外出有![]() 人,选择甲旅行社的费用为
人,选择甲旅行社的费用为![]() 元,选择乙旅行社的费用为
元,选择乙旅行社的费用为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式
的函数关系式
(3)该公司外出人数在什么范围内,选甲旅行社划算?