��Ŀ����
����Ŀ����ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]() ��
��![]() �˶�����
�˶�����![]() ��
��![]() ���غϣ����ٶ�Ϊÿ��
���غϣ����ٶ�Ϊÿ��![]() ��
��![]() ��
��![]() �ӳ�����һ�㣬���
�ӳ�����һ�㣬���![]() ����ͬ���ٶ���
����ͬ���ٶ���![]() ��
��![]() �ӳ��߷����˶�������
�ӳ��߷����˶�������![]() �غϣ�������
�غϣ�������![]() ��AB��
��AB��![]() ��
��


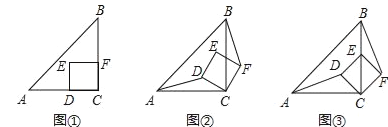
��1����ͼ1����![]() ��
��![]() �����P�˶������
�����P�˶������![]() .
.
��2���ڣ�1���������£���![]() ��F�����˶������У��߶�
��F�����˶������У��߶�![]() �����Ƿ����仯��������䣬���
�����Ƿ����仯��������䣬���![]() �ij�������仯����˵������.
�ij�������仯����˵������.
��3����ͼ3����![]() ʱ��ƽ���ı��ε������
ʱ��ƽ���ı��ε������![]() ����ô���˶����Ƿ����ijһʱ�̣���P��Q���ڵ�E�����ĶԳƣ������ڣ����a��ֵ���������ڣ�˵�����ɣ�
����ô���˶����Ƿ����ijһʱ�̣���P��Q���ڵ�E�����ĶԳƣ������ڣ����a��ֵ���������ڣ�˵�����ɣ�
���𰸡���1��2�룻��2��EF�ij��Ȳ��ᷢ���仯�����䳤��Ϊ3����3�����ڣ�a=5.
��������
��1����![]() cm����
cm����![]() cm���Ⱦ������Ƶá�ABC�ǵȱ������Σ���
cm���Ⱦ������Ƶá�ABC�ǵȱ������Σ���![]() ����һ���ɵ�
����һ���ɵ�![]() ��������30��ǵ�ֱ�������ε����ʵó�����x�ķ��̣��ⷽ�̼��ý����
��������30��ǵ�ֱ�������ε����ʵó�����x�ķ��̣��ⷽ�̼��ý����
��2����ͼ2������P��PH��BC��AB�ڵ�H����֪��APH�ǵȱ������Σ�������AAS֤�á�PEH�ա�QEB���Ӷ�HE=BE�����ڡ�APH�и��ݵȱ������ε����ʵó�AF=FH�����ǿɵ�EF��AB��������ϵ�����⼴�ý����
��3���������ijһʱ�̣�ʹP��Q���ڵ�E���ĶԳƣ���PE=QE����PG��BC��AB�ڵ�G����ͼ3��������AAS֤����PEG�ա�QEB���Ӷ���PG=AP����һ��������![]() �Ƴ�AC=BC������CM��AB�ڵ�M�����ɵ��������ε����ʿ����BM�ij���Ȼ�����ƽ���ı��ε�������CM�ij����ٸ��ݹ��ɶ����������a��ֵ.
�Ƴ�AC=BC������CM��AB�ڵ�M�����ɵ��������ε����ʿ����BM�ij���Ȼ�����ƽ���ı��ε�������CM�ij����ٸ��ݹ��ɶ����������a��ֵ.
�⣺��1����![]() cm����
cm����![]() cm����ͼ1��
cm����ͼ1��
��![]() ��
��![]() �����ABC�ǵȱ������Σ���
�����ABC�ǵȱ������Σ���![]() .
.
��![]() ����
����![]() ��
��
��![]() ����
����![]() �����
�����![]() ����
����![]() ��
��
���P�˶�2���![]() .
.
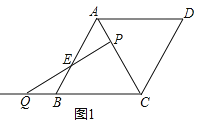
��2����ͼ2������P��PH��BC��AB�ڵ�H�����HPE=��BQE��
�ߡ�ABC�ǵȱ������Σ����APH�ǵȱ������Σ���AP=PH��
��AP=BQ����PH=BQ���֡ߡ�PEH=��QEB�����PEH�ա�QEB��AAS������HE=BE.
�ߡ�APH�ǵȱ������Σ�PF��AH����AF=FH��
��EF=EH+FH=![]() ��
��
��EF�ij��Ȳ��ᷢ���仯�����䳤��Ϊ3.
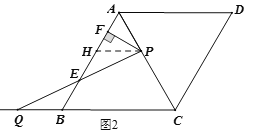
��3���������ijһʱ�̣�ʹP��Q���ڵ�E���ĶԳƣ���PE=QE��
��PG��BC��AB�ڵ�G����ͼ3�����PGE=��EBQ��
�֡ߡ�PEG=��BEQ��PE=QE��
���PEG�ա�QEB��AAS����
��PG=QB����PG=AP.
�ߡ�APG�ס�ACB����![]() ����AC=BC.
����AC=BC.
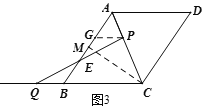
��CM��AB�ڵ�M����BM=AM=3cm��
��![]() ��
��![]() ����CM=4cm��
����CM=4cm��
��Rt��BCM�У����ݹ��ɶ�������![]() ��
��
��BC=5cm����a=5.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�������±��ش����⣺
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
��1��272.25��ƽ������������������
��2��![]() =��������������
=�������������� ![]() =��������������
=�������������� ![]() =������������
=������������
��3����![]() ����������Ϊa����4a����������
����������Ϊa����4a����������