Question

【题目】在平面直角坐标系中，反比例函数y＝（x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．

（1）求n的值；

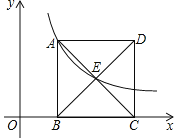
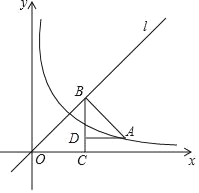
（2）如图，直线l为正比例函数y＝x的图象，点A在反比例函数y＝（x＞0，k＞0）的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的面积为S1，△ABD的面积为S2，求S1﹣S2的值．

Answer 1

【答案】（1）2（2）6

【解析】

（1）利用反比例函数图象上点的坐标特征得到n3n＝（n+1）2n，然后解方程可得n的值；

（2）设B（m，m），利用△OBC为等腰直角三角形得到∠OBC＝45°，再证明△ABD为等腰直角三角形，则可设BD＝AD＝t，所以A（m+t，m﹣t），把A（m+t，m﹣t）代入y＝中得到m2﹣t2＝12，然后利用整体代入的方法计算S1﹣S2．

解：（1）∵反比例函数y＝（x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．

∴n3n＝（n+1）2n，解得n＝2或n＝0（舍去），

∴n的值为2；

（2）反比例函数解析式为y＝，

设B（m，m），

∵OC＝BC＝m，

∴△OBC为等腰直角三角形，

∴∠OBC＝45°，

∵AB⊥OB，

∴∠ABO＝90°，

∴∠ABC＝45°，

∴△ABD为等腰直角三角形，

设BD＝AD＝t，则A（m+t，m﹣t），

∵A（m+t，m﹣t）在反比例函数解析式为y＝上，

∴（m+t）（m﹣t）＝12，

∴m2﹣t2＝12，

∴S1﹣S2＝＝6．