��Ŀ����
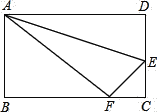
����Ŀ�����������Ŀ����������,����Ҫ�����֤������֪:��ͼ,E��BC���е�,��A��DB��,��
��BAE=��CDE,��֤:AB=CD
����:֤�������߶����,���õ�һ�㷽����Ӧ��ȫ�������λ���������ε��ж�������,�۲챾����Ҫ֤���������߶�,���Dz���ͬһ����������,�����Ƿֱ����ڵ�����������Ҳ��ȫ�ȡ����,Ҫ֤��AB=CD,���������ʵ��ĸ�����,����ȫ�������λ���������Ρ��ָ��������������Ӹ����ߵķ���,������ѡ���������ֶ�ԭ�����֤����
ͼ(1):�ӳ�DE��Fʹ��EF=DE
ͼ(2):��CG��DE��G,BF��DE��F��DE���ӳ�����F
ͼ(3):��C����CF��AB��DE���ӳ�����F.
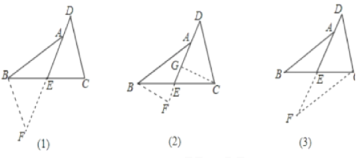
���𰸡�ѡ��1����3��֤����֤��������
��������
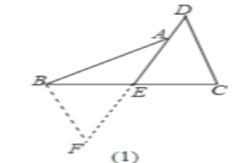
��ͼ(1)�ӳ�DE��Fʹ��EF=DE,֤����DCE�ա�FBE,�õ���CDE=��F,BF=DC,�������������ɵõ�����;��ͼ3,��C����CF��AB��DE���ӳ�����F,�õ���ABE�ա�FCE,AB=FC,�������������ɵõ�����,
��ͼ(1)�ӳ�DE��Fʹ��EF=DE
����DCE����FBE��,
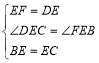
����DCE�ա� FBE��SAS)
��.��CDE=��F,BF=DC
�ߡ�BAB=��CDE
��BF=AB
��AB= CD
��ͼ3,��C����CF��AB��DE���ӳ�����F
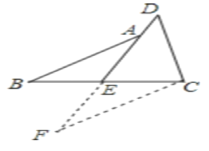
����ABE����FCE��
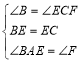
����ABE�ա� FCE(ASA),
��AB=FC
�ߡ�BAE=��CDE
���F=��CDE
��CD=CF
��AB=CD