题目内容
【题目】如图(1),在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上的一点,连接BO交AD于点F,OE⊥OB交BC边于点E.
(1)试说明:△ABF∽△COE.
(2)如图(2),当O为AC边的中点,且![]() 时,求
时,求![]() 的值.
的值.
(3)当O为AC边的中点,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

【答案】![]() 详见解析;
详见解析; ![]() (3)
(3)![]()
【解析】
(1)要求证:△ABF∽△COE.只要证明∠BAF=∠C,∠ABF=∠COE即可.
(2)作![]() 交BC于H,易证:△OEH∽△OFA,根据相似三角形的对应边的比相等,即可得出所求的值.同理可得(3)
交BC于H,易证:△OEH∽△OFA,根据相似三角形的对应边的比相等,即可得出所求的值.同理可得(3)![]()
(1)证明:∵AD⊥BC,
∴![]()
∵![]()
∴∠BAF=∠C.
∵OE⊥OB,
∴![]()
∵![]()
∴∠ABF=∠COE.
∴△ABF∽△COE.
(2)过O作AC垂线交BC于H,则OH![]() AB,
AB,
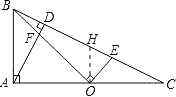
由(1)得∠ABF=∠COE,∠BAF=∠C.
∴∠AFB=∠OEC,
∴∠AFO=∠HEO,
而∠BAF=∠C,
∴∠FAO=∠EHO,
∴△OEH∽△OFA,
∴OF:OE=OA:OH
又∵O为AC的中点,OH![]() AB.
AB.
∴OH为△ABC的中位线,
∴![]()
而![]()
∴OA:OH=2:1,
∴OF:OE=2:1,即![]()
(3)![]()

练习册系列答案
相关题目






