题目内容
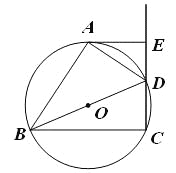
【题目】如图，四边形
中的三个顶点在⊙
上，
是优弧
上的一个动点（不与点
、
重合）．
（1）当圆心在
内部，∠ABO＋∠ADO=70°时，求∠BOD的度数；
（2）当点A在优弧BD上运动，四边形为平行四边形时，探究
与
的数量关系．
【答案】（1）140°；（2）当点A在优弧BD上运动，四边形
为平行四边形时，点O在∠BAD内部时，
+
=60°；点O在∠BAD外部时，|-|=60°．
【解析】
（1）连接OA，如图1，根据等腰三角形的性质得∠OAB=∠ABO，∠OAD=∠ADO，则∠OAB+∠OAD=∠ABO+∠ADO=70°，然后根据圆周角定理易得∠BOD=2∠BAD=140°；
（2）分点O在∠BAD内部和外部两种情形分类讨论：
①当点O在∠BAD内部时，
首先根据四边形OBCD为平行四边形，可得∠BOD=∠BCD，∠OBC=∠ODC；然后根据∠BAD+∠BCD=180°，∠BAD＝
∠BOD，求出∠BOD的度数，进而求出∠BAD的度数；最后根据平行四边形的性质，求出∠OBC、∠ODC的度数，再根据∠ABC+∠ADC=180°，求出∠OBA+∠ODA等于多少即可．
②当点O在∠BAD外部时：
Ⅰ、首先根据四边形OBCD为平行四边形，可得∠BOD=∠BCD，∠OBC=∠ODC；然后根据∠BAD+∠BCD=180°，∠BAD＝∠BOD，求出∠BOD的度数，进而求出∠BAD的度数；最后根据OA=OD，OA=OB，判断出∠OAD=∠ODA，∠OAB=∠OBA，进而判断出∠OBA=∠ODA+60°即可．
Ⅱ、首先根据四边形OBCD为平行四边形，可得∠BOD=∠BCD，∠OBC=∠ODC；然后根据∠BAD+∠BCD=180°，∠BAD＝∠BOD，求出∠BOD的度数，进而求出∠BAD的度数；最后根据OA=OD，OA=OB，判断出∠OAD=∠ODA，∠OAB=∠OBA，进而判断出∠ODA=∠OBA+60°即可．
（1）连接OA，如图1，
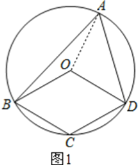
∵OA=OB，OA=OD，
∵∠OAB=∠ABO，∠OAD=∠ADO，
∴∠OAB+∠OAD=∠ABO+∠ADO=70°，即∠BAD=70°，
∴∠BOD=2∠BAD=140°；
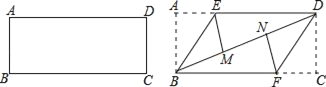
（2）①如图2，
，
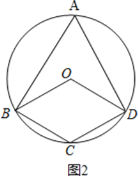∵四边形OBCD为平行四边形，
∴∠BOD=∠BCD，∠OBC=∠ODC，
又∵∠BAD+∠BCD=180°，∠BAD＝∠BOD，
∴∠BOD+∠BOD＝180°，
∴∠BOD=120°，∠BAD=120°÷2=60°，
∴∠OBC=∠ODC=180°-120°=60°，
又∵∠ABC+∠ADC=180°，
∴∠OBA+∠ODA=180°-（∠OBC+∠ODC）
=180°-（60°+60°）
=180°-120°
=60°
②Ⅰ、如图3，
，
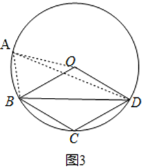∵四边形OBCD为平行四边形，
∴∠BOD=∠BCD，∠OBC=∠ODC，
又∵∠BAD+∠BCD=180°，∠BAD＝∠BOD，
∴∠BOD+∠BOD＝180°，
∴∠BOD=120°，∠BAD=120°÷2=60°，
∴∠OAB=∠OAD+∠BAD=∠OAD+60°，
∵OA=OD，OA=OB，
∴∠OAD=∠ODA，∠OAB=∠OBA，
∴∠OBA-∠ODA=60°．
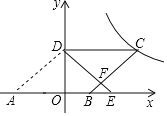
Ⅱ、如图4，
，
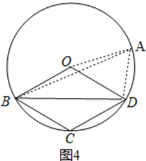∵四边形OBCD为平行四边形，
∴∠BOD=∠BCD，∠OBC=∠ODC，
又∵∠BAD+∠BCD=180°，∠BAD＝∠BOD，
∴∠BOD+∠BOD＝180°，
∴∠BOD=120°，∠BAD=120°÷2=60°，
∴∠OAB=∠OAD-∠BAD=∠OAD-60°，
∵OA=OD，OA=OB，
∴∠OAD=∠ODA，∠OAB=∠OBA，
∴∠OBA=∠ODA-60°，
即∠ODA-∠OBA=60°．
所以，当点A在优弧BD上运动，四边形为平行四边形时，点O在∠BAD内部时，+=60°；点O在∠BAD外部时，|-|=60°．
