题目内容
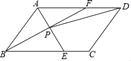
【题目】如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
【答案】A
【解析】
作PH⊥AD于H,可得四边形ABEF是菱形,∠ABC=60°,AB=4,得到AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,从而得到PH=![]() ,DH=5,然后利用锐角三角函数的定义求解即可.
,DH=5,然后利用锐角三角函数的定义求解即可.
解:作PH⊥AD于H,
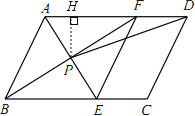
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
∵∠ABC=60°,AB=4,
∴AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=![]() AB=2,
AB=2,
∴PH=![]() ,DH=5,
,DH=5,
∴tan∠ADP=![]() =
=![]() .
.
故选:A.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润(元/件) | B型利润(元/件) | |
甲店 | 180 | 150 |
乙店 | 120 | 110 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并写出x的取值范围;
(2)若要求总利润超过14960元,有多少种不同分配方案?请列出具体方案;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润,甲店的B型产品以及乙店的A,B型产品的每件利润不变,该公司如何设计分配方案,使总利润达到最大?