题目内容
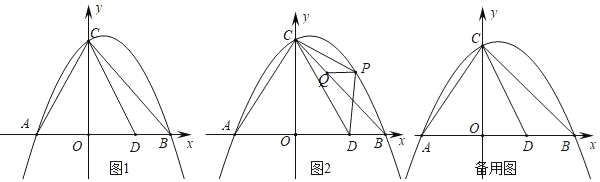
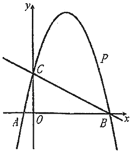
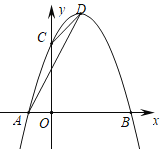
【题目】如图，抛物线y＝ax2+bx+3与x轴交于A（﹣1，0）和B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点，分别连接AC、CD、AD．
（1）求抛物线的函数解析式以及顶点D的坐标；
（2）在抛物线上取一点P（不与点C重合）、并分别连接PA、PD，当△PAD的面积与△ACD的面积相等时，求点P的坐标：
【答案】（1）抛物线的解析式为y＝﹣x2+2x+3，顶点D的坐标为（1，4）；（2）点P的坐标为（
，2+1），（﹣，﹣2+1）．
【解析】
（1）根据抛物线y＝ax2+bx+3与x轴交于A（﹣1，0）和B（3，0）两点，可以求得该抛物线的解析式，然后化为顶点式即可求得顶点D的坐标；
（2）根据题意，作出合适的辅助线，利用平移的性质即可求得点P的坐标．
解：（1）设抛物线的函数解析式为y＝a（x+1）（x﹣3），
∵y＝ax2+bx+3，
∴﹣3a＝3，得a＝﹣1，
∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3＝﹣（x﹣1）2+4，
即该抛物线的解析式为y＝﹣x2+2x+3，顶点D的坐标为（1，4）；
（2）∵抛物线的解析式为y＝﹣x2+2x+3，与y轴交于点C，
∴点C的坐标为（0，3），
设过点A（﹣1，0）和点D（1，4）的直线解析式为y＝kx+m，
，得
，
即直线AD的函数解析式为y＝2x+2，
设直线AD与y轴交于点E，则点E的坐标为（0，2），
则CE＝OC﹣OE＝3﹣2＝1，
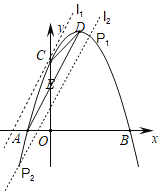
过点C作直线l1∥AD，则直线l1的解析式为y＝2x+3，
令﹣x2+2x+3＝2x+3，得x1＝x2＝0，
即抛物线与直线l1只有一个交点为（0，3），在直线AD上方的抛物线上不存在△PAD的面积与△ACD的面积相等的点P；
将直线AD沿y轴向下平移一个单位长度得到直线l2，则直线l2的解析式为y＝2x+1，
令﹣x2+2x+3＝2x+1，得x3＝，x4＝﹣，
则点P1为（，2+1），点P2为（﹣，﹣2+1），
即点P的坐标为（，2+1），（﹣，﹣2+1）．
