题目内容
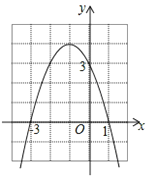
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 两点,直线
两点,直线![]() 与y 轴交于点
与y 轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是
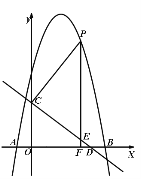
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() 。
。
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点、是否存在点
的对称点、是否存在点![]() ,使点
,使点![]() 落在y轴上?若存在,求出相应的点
落在y轴上?若存在,求出相应的点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
【答案】(1)y=-x2+4x+5.(2) m=2或m=![]() .(3) 点P坐标为(-
.(3) 点P坐标为(-![]() ,
,![]() ),(4,5),(3-
),(4,5),(3-![]() ,2
,2![]() -3).
-3).
【解析】
试题(1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解;
(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到点P坐标.
试题解析:(1)将点A、B坐标代入抛物线解析式,得:
![]() ,
,
解得![]() ,
,
∴抛物线的解析式为:y=-x2+4x+5.
(2)∵点P的横坐标为m,
∴P(m,-m2+4m+5),E(m,-![]() m+3),F(m,0).
m+3),F(m,0).
∴PE=|yP-yE|=|(-m2+4m+5)-(-![]() m+3)|=|-m2+
m+3)|=|-m2+![]() m+2|,
m+2|,
EF=|yE-yF|=|(-![]() m+3)-0|=|-
m+3)-0|=|-![]() m+3|.
m+3|.
由题意,PE=5EF,即:|-m2+![]() m+2|=5|-
m+2|=5|-![]() m+3|=|-
m+3|=|-![]() m+15|
m+15|
①若-m2+![]() m+2=-
m+2=-![]() m+15,整理得:2m2-17m+26=0,
m+15,整理得:2m2-17m+26=0,
解得:m=2或m=![]() ;
;
②若-m2+![]() m+2=-(-
m+2=-(-![]() m+15),整理得:m2-m-17=0,
m+15),整理得:m2-m-17=0,
解得:m=![]() 或m=
或m=![]() .
.
由题意,m的取值范围为:0<m<5,故m=![]() 、m=
、m=![]() 这两个解均舍去.
这两个解均舍去.
∴m=2或m=![]() .
.
(3)假设存在.
作出示意图如下:
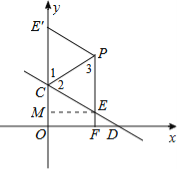
∵点E、E′关于直线PC对称,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y轴,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四边形PECE′是菱形.
当四边形PECE′是菱形存在时,
由直线CD解析式y=-![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,
∴![]() ,
,
即![]() ,
,
解得CE=![]() |m|,
|m|,
∴PE=CE=![]() |m|,
|m|,
又由(2)可知:PE=|-m2+![]() m+2|
m+2|
∴|-m2+![]() m+2|=
m+2|=![]() |m|.
|m|.
①若-m2+![]() m+2=
m+2=![]() m,整理得:2m2-7m-4=0,
m,整理得:2m2-7m-4=0,
解得m=4或m=-![]() ;
;
②若-m2+![]() m+2=-
m+2=-![]() m,整理得:m2-6m-2=0,解得m1=3+
m,整理得:m2-6m-2=0,解得m1=3+![]() ,m2=3-
,m2=3-![]() .
.
由题意,m的取值范围为:-1<m<5,故m=3+![]() 这个解舍去.
这个解舍去.
当四边形PECE′是菱形这一条件不存在时,
此时P点横坐标为0,E,C,E'三点重合与y轴上,菱形不存在,即P点为(0,5).
综上所述,存在满足条件的点P,可求得点P坐标为(-![]() ,
,![]() ),(4,5),(3-
),(4,5),(3-![]() ,2
,2![]() -3)
-3)

【题目】为了传承中华优秀传统文化,某校学生会组织了一次全校1200名学生参加的“汉字听写”大赛,并设成绩优胜奖.
赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中100名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.10 |
60≤x<70 | 25 | 0.25 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.20 |
90≤x≤100 | 15 | 0.15 |
成绩在70≤x<80这一组的是:
70 70 71 71 71 72 72 73 73 73 73 75 75 75 75 76 76 76 76 76 76 76 76 77 77 78 78 78 79 79
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在78分以上(含78分)的学生获得优胜奖,则该校参加这次比赛的1200名学生中获优胜奖的约有多少人?