题目内容
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= . 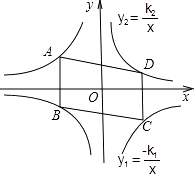
【答案】8
【解析】解:在ABCD中,AB∥CD,AB=CD(平行四边形的对应边平行且相等),故设A(x,y1)、B(x、y2),则根据反比例函数的图象关于原点对称的性质知,C(﹣x,﹣y1)、D(﹣x、﹣y2).
∵A在双曲线y1=﹣ ![]() 上,B在双曲线y2=
上,B在双曲线y2= ![]() 上,
上,
∴x=﹣ ![]() ,x=
,x= ![]() ,
,
∴﹣ ![]() =
= ![]() ;
;
又∵k1=2k2(k1>0),
∴y1=﹣2y2;
∵SABCD=24,
∴ ![]() |2x|=6|y2x|=24,
|2x|=6|y2x|=24,
解得,y2x=±4,
∵双曲线y2= ![]() 位于第一、三象限,
位于第一、三象限,
∴k2=4,
∴k1=2k2=8
故答案是:8.

【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目