题目内容
【题目】如图1,矩形![]() 顶点
顶点![]() 的坐标为
的坐标为![]() ,定点
,定点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴的正方向匀速运动,动点
轴的正方向匀速运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴的负方向匀速运动,
轴的负方向匀速运动,![]() 两点同时运动,相遇时停止.在运动过程中,以
两点同时运动,相遇时停止.在运动过程中,以![]() 为斜边在轴上方作等腰直角三角形
为斜边在轴上方作等腰直角三角形![]() ,设运动时间为
,设运动时间为![]() 秒,
秒,![]() 和矩形
和矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
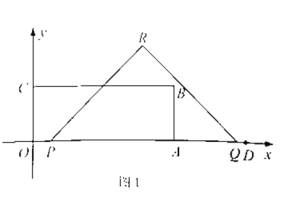
关于![]() 的函数如图2所示(其中
的函数如图2所示(其中![]() ,
,![]() ,
,![]() 时,函数的解析式不同).
时,函数的解析式不同).

![]() 当
当![]() 时,
时,![]() 的边
的边![]() 经过点
经过点![]() ;
;
![]() 求
求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)S=
【解析】
(1)![]() PQR的边QR经过点B时,
PQR的边QR经过点B时,![]() 构成等腰直角三角形,则由AB=AQ,列方程求出t值即可.
构成等腰直角三角形,则由AB=AQ,列方程求出t值即可.
(2)在图形运动的过程中,有三种情形,当1<t≤2时,当1<t≤2时,当2<t≤4时,进行分类讨论求出答案.
解:![]()
![]() PQR的边QR经过点B时,
PQR的边QR经过点B时,![]() 构成等腰直角三角形;
构成等腰直角三角形;
![]() AB=AQ,即3=4-t
AB=AQ,即3=4-t
![]()
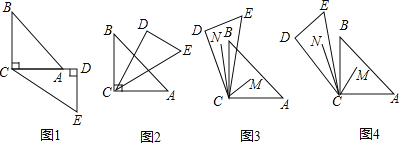
![]() ①当
①当![]() 时,如图
时,如图![]()
设![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
则![]()
![]()
![]()
![]()

②当![]() 时,如图
时,如图![]()
设![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]()
则![]() ,
,![]()
![]()
![]()
![]()

③当![]() 时,如图
时,如图![]()
设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]()
![]()
![]()
![]()
![]()

综上所述,![]() 关于
关于![]() 的函数关系式为:S=
的函数关系式为:S=

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
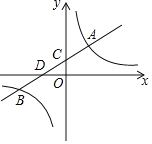
【题目】下表给出三种上宽带网的收费方式.
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
![]() 设月上网时间为
设月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() ,直接写出
,直接写出![]() 的解析式,并写出自变量
的解析式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 填空:
填空:![]() 当上网时间 时,选择方式
当上网时间 时,选择方式![]() 最省钱;
最省钱;
![]() 当上网时间 时,选择方式
当上网时间 时,选择方式![]() 最省钱;
最省钱;
![]() 当上网时间 时,选择方式
当上网时间 时,选择方式![]() 最省钱;
最省钱;