Question

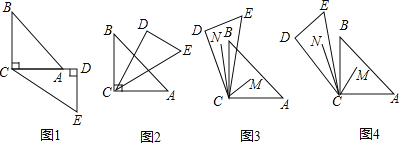
【题目】将一副三角板如图①摆放，，现将绕点以的速度逆时针旋转，旋转时间为.

（1）为多少时，恰好平分？请在图②中自己画图，并说明理由；

（2）当6﹤t﹤8时，平分∠ACE，平分，求，在图中③中完成；

（3）当8﹤t﹤12时，（2）中的结论是否发生变化？请在图④中完成.

Answer 1

【答案】（1）；（2）；（3）不变，.

【解析】

（1）利用角平分线的性质，求出∠BCD=∠DCE=30°，则∠DCA=60°，进而得出t的值，（2）当时，在内部，，，再利用角平分线，分别表示出∠ACM和∠DCN，进而表示出∠MCN，化简即可，（3）同（2）.

解：

（1）当平分时，

∠BCD=∠DCE=30°，

∴∠DCA=60°，

∴（s）,

（2）当时，在内部，

且，，

∵CM平分∠ACE，平分，

∴，，

∴.

（3）不变，，理由如下，

当8﹤t﹤12时，CE在CB的左侧，

且，，

∵CM平分∠ACE，平分，

∴，，

∴.