题目内容
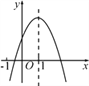
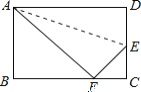
【题目】如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_____.

【答案】40°
【解析】试题分析:先根据三角形外角性质计算出∠EBF=∠A+∠E=85°,再根据圆内接四边形的性质计算出∠BCD=180°﹣∠A=125°,然后再根据三角形外角性质求∠F.
解:∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
故答案为40°.
考点:圆内接四边形的性质;三角形内角和定理.
【题型】填空题
【结束】
17
【题目】某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种 棵橘子树,橘子总个数最多.
【答案】10.
【解析】
试题分析:假设果园增种x棵橘子树,那么果园共有(x+100)棵橘子树,∵每多种一棵树,平均每棵树就会少结5个橘子,∴这时平均每棵树就会少结5x个橘子,则平均每棵树结(600﹣5x)个橘子.∵果园橘子的总产量为y,∴则![]() ,∴当
,∴当![]() 棵时,橘子总个数最多.故答案为:10.
棵时,橘子总个数最多.故答案为:10.

练习册系列答案
相关题目