ΧβΡΩΡΎ»ί
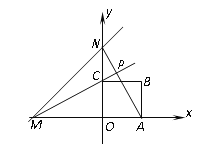
ΓΨΧβΡΩΓΩΨΘ÷ί –Ρ≥Υ°≤ζ―χ÷≥ΜßΫχ–––ΓΝζœΚ―χ÷≥Θ°“―÷ΣΟΩ«ßΩΥ–ΓΝζœΚ―χ÷≥≥…±ΨΈΣ6‘ΣΘ§‘Ύ’ϊΗωœζ έΆζΦΨΒΡ80ΧλάοΘ§œζ έΒΞΦέpΘ®‘Σ/«ßΩΥΘ©”κ ±ΦδΒΎtΘ®ΧλΘ©÷°ΦδΒΡΚ· ΐΙΊœΒΈΣΘΚ![]() Θ®1ΓήtΓή80Θ§tΈΣ’ϊ ΐΘ©Θ§»’œζ έΝΩyΘ®«ßΩΥΘ©”κ ±ΦδΒΎtΘ®ΧλΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘΚ
Θ®1ΓήtΓή80Θ§tΈΣ’ϊ ΐΘ©Θ§»’œζ έΝΩyΘ®«ßΩΥΘ©”κ ±ΦδΒΎtΘ®ΧλΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘΚ
Θ®1Θ©«σ»’œζ έΝΩy”κ ±ΦδtΒΡΚ· ΐΙΊœΒ ΫΘΩ
Θ®2Θ©ΡΡ“ΜΧλΒΡ»’œζ έάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
Θ®3Θ©‘Ύ ΒΦ œζ έΒΡ«Α40Χλ÷–Θ§ΗΟ―χ÷≥ΜßΨωΕ®ΟΩœζ έ1«ßΩΥ–ΓΝζœΚΘ§ΨΆΨη‘υmΘ®mΘΦ7Θ©‘ΣΗχ¥εάοΒΡΧΊάßΜßΘ°‘Ύ’β«Α40Χλ÷–Θ§ΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±ΦδtΒΡ‘ω¥σΕχ‘ω¥σΘ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
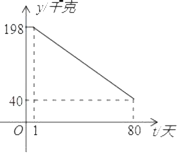
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ2tΘΪ200Θ®1ΓήtΓή80Θ§tΈΣ’ϊ ΐΘ©ΘΜΘ®2Θ©ΒΎ30ΧλΒΡ»’œζ έάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «2450‘ΣΘΜΘ®3Θ©5ΓήmΘΦ7Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΚ· ΐΆΦœσΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©…η»’œζ έάϊ»σΈΣWΘ§ΗυΨίΓΑ»’œζ έάϊ»σΘΫΘ® έΦέ≥…±ΨΘ©ΓΝ»’œζ έΝΩΓ±Ν–≥ωΚ· ΐΫβΈω ΫΘ§”…Εΰ¥ΈΚ· ΐΒΡ–‘÷ «σΒΟΉν÷ΒΦ¥Ω…≈–ΕœΘΜ
Θ®3Θ©…η»’œζ έάϊ»σΈΣWΘ§ΗυΨίΓΑ»’œζ έάϊ»σΘΫΘ® έΦέ≥…±ΨΨηΩνΘ©ΓΝ»’œζ έΝΩΓ±Ν–≥ωΚ· ΐΫβΈω ΫΘ§άϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΫαΚœ«Α40ΧλΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±ΦδtΒΡ‘ω¥σΕχ‘ω¥σ«σΫβΩ…ΒΟΘ°
ΫβΘΚΘ®1Θ©…ηΚ· ΐΙΊœΒ ΫΈΣyΘΫktΘΪbΘ®kΓΌ0Θ©Θ§
ΫΪΘ®1Θ§198Θ©ΓΔΘ®80Θ§40Θ©¥ζ»κΘ§ΒΟΘΚ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ»’œζ έΝΩy”κ ±ΦδtΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚyΘΫ2tΘΪ200Θ®1ΓήtΓή80Θ§tΈΣ’ϊ ΐΘ©ΘΜ
Θ®2Θ©…η»’œζ έάϊ»σΈΣWΘ§
‘ρ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύΒ±t=30 ±Θ§WΉν¥σΘΫ2450ΘΜ
¥πΘΚΒΎ30ΧλΒΡ»’œζ έάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «2450‘ΣΘΜ
Θ®3Θ©…η»’œζ έάϊ»σΈΣWΘ§
ΗυΨίΧβ“βΒΟΘΚ![]() Θ§
Θ§
ΤδΚ· ΐΆΦœσΒΡΕ‘≥Τ÷αΈΣtΘΫ2mΘΪ30Θ§
ΓΏΒ±1ΓήtΓή40 ±Θ§WΥφtΒΡ‘ω¥σΕχ‘ω¥σΘ§
Γύ”…Εΰ¥ΈΚ· ΐΒΡΆΦœσΦΑΤδ–‘÷ Ω…÷Σ2mΘΪ30Γί40Θ§
ΫβΒΟΘΚmΓί5Θ§
”÷ΓΏmΘΦ7Θ§
Γύ5ΓήmΘΦ7Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
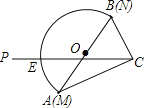
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥Ά®―ΕΙΪΥΨΙφΕ®ΘΚ“ΜΟϊΩΆΜß»γΙϊ“ΜΗω‘¬ΒΡΆ®ΜΑ ±Φδ≤Μ≥§Ιΐ![]() Ζ÷÷”Θ§Ρ«Ο¥’βΗω‘¬’βΟϊΩΆΜß÷Μ“ΣΫΜ10‘ΣΆ®ΜΑΖ―ΘΜ»γΙϊ≥§Ιΐ
Ζ÷÷”Θ§Ρ«Ο¥’βΗω‘¬’βΟϊΩΆΜß÷Μ“ΣΫΜ10‘ΣΆ®ΜΑΖ―ΘΜ»γΙϊ≥§Ιΐ![]() Ζ÷÷”Θ§Ρ«Ο¥’βΗω‘¬≥ΐΝΥ»‘“ΣΫΜ10‘ΣΆ®ΜΑΖ―ΆβΘ§≥§Ιΐ≤ΩΖ÷ΜΙ“ΣΑ¥ΟΩΖ÷÷”
Ζ÷÷”Θ§Ρ«Ο¥’βΗω‘¬≥ΐΝΥ»‘“ΣΫΜ10‘ΣΆ®ΜΑΖ―ΆβΘ§≥§Ιΐ≤ΩΖ÷ΜΙ“ΣΑ¥ΟΩΖ÷÷”![]() ‘ΣΫΜΖ―Θ°
‘ΣΫΜΖ―Θ°
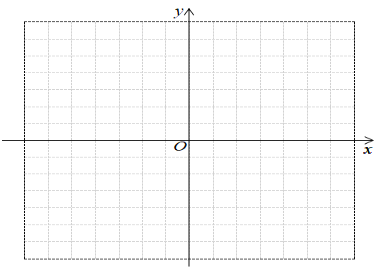
Θ®ΔώΘ©Ρ≥ΟϊΩΆΜß7‘¬ΖίΆ®ΜΑ90Ζ÷÷”Θ§≥§ΙΐΝΥΙφΕ®ΒΡ![]() Ζ÷÷”Θ§‘ρ≥§Ιΐ≤ΩΖ÷”ΠΫΜΆ®ΜΑΖ―______‘ΣΘ®”ΟΚ§
Ζ÷÷”Θ§‘ρ≥§Ιΐ≤ΩΖ÷”ΠΫΜΆ®ΜΑΖ―______‘ΣΘ®”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
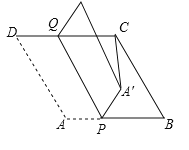
Θ®ΔρΘ©œ¬±μ±μ ΨΡ≥ΟϊΩΆΜß8‘¬ΖίΓΔ9‘¬ΖίΒΡΆ®ΜΑ«ιΩωΚΆΫΜΖ―«ιΩωΘΚ
‘¬Ζί | Ά®ΜΑ ±Φδ/Ζ÷÷” | Ά®ΜΑΖ―Ήή ΐ/‘Σ |
8‘¬Ζί | 80 | 25 |
9‘¬Ζί | 45 | 10 |
ΗυΨί…œ±μΒΡ ΐΨίΘ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°