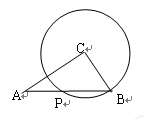
题目内容
已知:如图,⊙ 的直径
的直径 与弦
与弦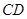 (不是直径)交于点
(不是直径)交于点 ,若
,若 =2,
=2, ,求
,求 的长.
的长.

 的直径
的直径 与弦
与弦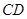 (不是直径)交于点
(不是直径)交于点 ,若
,若 =2,
=2, ,求
,求 的长.
的长.
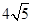 .
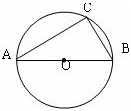
.试题分析:连结OD,设⊙O的半径为R,根据AB是⊙O的直径,且CF=DF,在Rt△OFD中,根据勾股定理可得出AF的长,在Rt△ACF中,根据勾股定理可求出AC的长.
试题解析:如图,连结OD,设⊙O的半径为R,

∵AB是⊙O的直径,且CF=DF,
∴AB⊥CD,
∵OB=R BF=2,则OF=R-2,
在Rt△OFD中,
由勾股定理得:R2=(R-2)2+42,解得:R=5
∴AF=8.
在Rt△ACF中
由勾股定理得:AC=
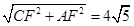 .
.考点:1.垂径定理;2.勾股定理.

练习册系列答案
相关题目
 中,
中, ,以AC为直径的⊙O交AB于点D,E是BC的中点.
,以AC为直径的⊙O交AB于点D,E是BC的中点.






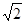 ,BC=1,若以C为圆心,CB为半径的圆交AB于点P,则AP =_____
,BC=1,若以C为圆心,CB为半径的圆交AB于点P,则AP =_____