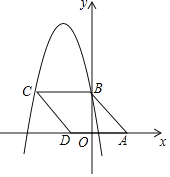题目内容
【题目】如图1，正方形MNPQ网格中，每个小方格的边长都相等，正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上．
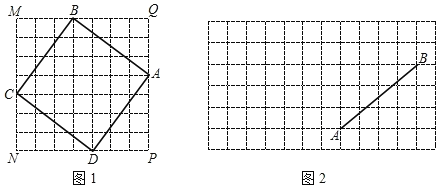
（1）设正方形MNPQ网格内的每个小方格的边长为1，求：正方形ABCD的面积；
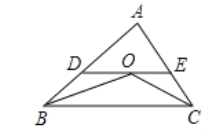
（2）①在图2中画出以AB为一条直角边的等腰直角△ABC，且点C在小正方形的顶点上；
②在图2中画出以AB为一边的菱形ABDE，且点D和点E均在小正方形的顶点上，菱形ABDE的面积为15，连接CE，请直接写出线段CE的长．
【答案】（1）25；（2）①作图见解析；②
．
【解析】
（1）根据正方形ABCD的面积等于所在大正方形的面积减去四个相邻三角形面积列式计算即可；
（2）①按要求做出图形即可；②按要求画出图形即可，CE长度根据勾股定理即可求出.
（1）∵MQ=7，∴S正方形MNPQ=72=49，∴S正方形ABCD=S正方形MNPQ﹣4S△ABQ=49﹣4×6=25．
（2）如图所示，①△ABC即为所求，②菱形ABDE即为所求，如图，CE在一个直角边分别为2和4的直角三角形中，根据勾股定理可知：
．
练习册系列答案
相关题目
