题目内容
如图，已知Rt△ABC中，∠ABC=90°，∠BAC=30°，AB=2
cm，将△ABC绕顶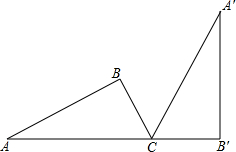
点C顺时针旋转至△A′B′C′的位置，且A、C、B′三点在同一条直线上，则点A经过的最短路线的长度是（ ）cm．
| 3 |
点C顺时针旋转至△A′B′C′的位置，且A、C、B′三点在同一条直线上，则点A经过的最短路线的长度是（ ）cm．| A、8 | ||
B、4
| ||
C、
| ||
D、
|
分析：点A经过的最短路线的长度是一段弧长，圆心是C，半径是AC，旋转的度数是120度，由特殊三角函数可求得AC=4，所以根据弧长公式可得．
解答：解：弧长=
=
π．
故选D．
| 120π×4 |
| 180 |
| 8 |
| 3 |
故选D．
点评：本题的关键是找准圆心角和半径求弧长．
练习册系列答案
相关题目
22、如图，已知Rt△ABC，AB=AC，∠ABC的平分线BD交AC于点D，BD的垂直平分线分别交AB，BC于点E、F，CD=CG．
E，交⊙O于点F，且AE=BE．
5、如图，已知Rt△ABC中，∠BAC=90°，AB=AC，P是BC延长线上一点，PE⊥AB交BA延长线于E，PF⊥AC交AC延长线于F，D为BC中点，连接DE，DF．求证：DE=DF．
如图，已知Rt△ABC中，∠CAB=30°，BC=5．过点A做AE⊥AB，且AE=15，连接BE交AC于点P．
如图，已知Rt△ABC中∠A=90°，AB=3，AC=4．将其沿边AB向右平移2个单位得到△FGE，则四边形ACEG的面积为