题目内容
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.分析:连接AD,由题意可判断出四边形AEPF是矩形,再根据矩形的性质可得出AE=FP,由Rt△ABC中,∠BAC=90°,AB=AC,D为BC中点可得出AD=BC,∠1=∠2=45°=∠3,再由全等三角形的判定定理可得出△ADE≌△CDF,进而可得出结论.
解答: 证明:连接AD(如图),
证明:连接AD(如图),
∵∠BAC=90°,PE⊥AB,PF⊥AC
∴四边形AEPF是矩形,
∴AE=FP,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=DC,∠1=∠2=45°=∠3,
∴∠EAD=∠FCD=135°,∠CPF=45°=∠3,
∴CF=PF=AE,
∴△ADE≌△CDF(SAS)
∴DE=DF.
 证明:连接AD(如图),
证明:连接AD(如图),∵∠BAC=90°,PE⊥AB,PF⊥AC
∴四边形AEPF是矩形,
∴AE=FP,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=DC,∠1=∠2=45°=∠3,
∴∠EAD=∠FCD=135°,∠CPF=45°=∠3,
∴CF=PF=AE,
∴△ADE≌△CDF(SAS)
∴DE=DF.
点评:本题考查的是矩形的判定与性质、全等三角形的判定与性质、三角形内角和定理,涉及面较广,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.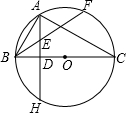 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为