ΧβΡΩΡΎ»ί
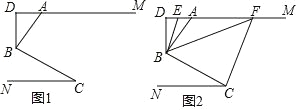
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§E «AB…œ“ΜΒψΘ§F «AD―”≥ΛœΏ…œ“ΜΒψΘ§«“DFΘΫBEΘ°“Ή÷ΛΘΚCEΘΫCFΘ°

Θ®1Θ©‘ΎΆΦ1÷–Θ§»τG‘ΎAD…œΘ§«“ΓœGCEΘΫ45ΓψΘ° ‘≤¬œκGEΘ§BEΘ§GD»ΐœΏΕΈ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
Θ®2Θ©‘Υ”ΟΘ®1Θ©÷–Ϋβ¥πΥυΜΐάέΒΡΨ≠―ιΚΆ÷Σ ΕΘ§Άξ≥…œ¬ΟφΝΫΧβΘΚ
ΔΌ»γΆΦ2Θ§‘ΎΥΡ±Ώ–ΈABCD÷–ΓœBΘΫΓœDΘΫ90ΓψΘ§BCΘΫCDΘ§ΒψEΘ§ΒψGΖ÷±π «AB±ΏΘ§AD±Ώ…œΒΡΕ·ΒψΘ°»τΓœBCDΘΫΠΝΘ§ΓœECGΘΫΠ¬Θ§ ‘ΧΫΥςΒ±ΠΝΚΆΠ¬¬ζΉψ ≤Ο¥ΙΊœΒ ±Θ§ΆΦ1÷–GEΘ§BEΘ§GD»ΐœΏΕΈ÷°ΦδΒΡΙΊœΒ»‘»Μ≥…ΝΔΘ§≤ΔΥΒΟςάμ”…Θ°
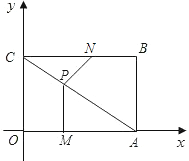
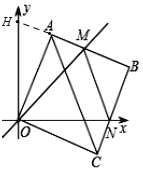
ΔΎ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξ÷–Θ§±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈOABCΒΡΝΫΕΞΒψAΘ§CΖ÷±π‘Ύy÷αΓΔx÷αΒΡ’ΐΑκ÷α…œΘ§ΒψO‘Ύ‘≠ΒψΘ°œ÷ΫΪ’ΐΖΫ–ΈOABC»ΤOΒψΥ≥ ±’κ–ΐΉΣΘ§Β±AΒψΒΎ“Μ¥Έ¬δ‘Ύ÷±œΏyΘΫx…œ ±ΆΘ÷Ι–ΐΉΣΘ§–ΐΉΣΙΐ≥Χ÷–Θ§AB±ΏΫΜ÷±œΏyΘΫx”ΎΒψMΘ§BC±ΏΫΜx÷α”ΎΒψNΘ®»γΆΦ3Θ©Θ°…ηΓςMBNΒΡ÷ή≥ΛΈΣpΘ§‘Ύ–ΐΉΣ’ΐΖΫ–ΈOABCΒΡΙΐ≥Χ÷–Θ§p÷Β «Ζώ”–±δΜ·ΘΩ»τ≤Μ±δΘ§«κ÷±Ϋ”–¥≥ωΫα¬έΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©GE=GD+DFΘ§÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©Π¬=2ΠΝ ±Θ§GE=GD+DF»‘»Μ≥…ΝΔΘ§άμ”…ΦϊΫβΈωΘΜΘ®3Θ©ΓςBMNΒΡ÷ή≥ΛΟΜ”–±δΜ·Θ§÷ή≥ΛΈΣ2Θ°
ΓΨΫβΈωΓΩ
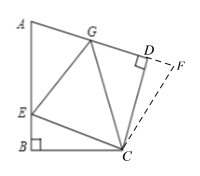
Θ®1Θ©”…’ΐΖΫ–ΈΒΡ–‘÷ Ω…ΒΟΓœBCD=ΓœB=ΓœADC=90ΓψΘ§BC=CDΘ§”…ΓœCEG=45ΓψΩ…ΒΟΓœBCE+ΓœDCG=45ΓψΘ§άϊ”ΟSASΩ…÷ΛΟςΓςBCEΓ’ΓςDCFΘ§Ω…ΒΟΓœBCE=ΓœDCFΘ§CE=CFΘ§Φ¥Ω…ΒΟ≥ωΓœFCG=45ΓψΘ§Ω…ΒΟΓœFCG=ΓœGCEΘ§άϊ”ΟSASΩ…÷ΛΟςΓςCEGΓ’ΓςCFGΘ§Ω…ΒΟEG=FGΘ§ΗυΨίBE=DFΦ¥Ω…ΒΟ≥ωGE=GD+BEΘΜ
Θ®2Θ©ΔΌ»γΆΦΘ§―”≥ΛADΒΫFΘ§ ΙDF=BEΘ§Ν§Ϋ”CFΘ§άϊ”ΟSASΩ…÷ΛΟςΓςBCEΓ’ΓςDCFΘ§Ω…ΒΟΓœBCE=ΓœDCFΘ§CE=CFΘ§ΗυΨίGE=GD+BEΩ…ΒΟEG=GFΘ§άϊ”ΟSSSΩ…÷ΛΟςΓςCEGΓ’ΓςCFGΘ§Ω…ΒΟΓœGCF=ΓœGCEΘ§”…ΓœGCF=ΓœGCD+ΓœDCFΩ…ΒΟΓœGCE=ΓœGCD+ΓœBCEΘ§Φ¥Ω…ΒΟ≥ωΓœBCD=2ΓœGCEΘ§Ω…ΒΟ¥πΑΗΘΜ
ΔΎ»γΆΦΘ§―”≥ΛBAΘ§ΫΜy÷α”ΎHΘ§”…–ΐΉΣΒΡ–‘÷ Ω…ΒΟΓœHOA=ΓœNOCΘ§άϊ”ΟASAΩ…÷ΛΟςΓςHOAΓ’ΓςNOCΘ§Ω…ΒΟAH=CNΘ§OH=ONΘ§”…÷±œΏOMΒΡΫβΈω ΫΩ…ΒΟΓœHAM=ΓœMON=45ΓψΘ§άϊ”ΟSASΩ…÷ΛΟςΓςHOMΓ’ΓςNOMΘ§Ω…ΒΟHM=MNΘ§Ω…ΒΟMN=AM+CNΘ§Φ¥Ω…ΒΟ≥ωΓςMBNΒΡ÷ή≥Λp=AB+BC=2Θ§Φ¥Ω…÷ΛΟςΓςMBNΒΡ÷ή≥ΛΟΜ”–±δΜ·Θ°
Θ®1Θ©GE=GD+DFΘ§άμ”…»γœ¬ΘΚ
ΓΏABCD «’ΐΖΫ–ΈΘ§
ΓύΓœBCD=ΓœB=ΓœADC=90ΓψΘ§BC=CDΘ§
‘ΎΓςBCEΚΆΓςDCF÷–Θ§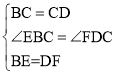 Θ§
Θ§
ΓύΓςBCEΓ’ΓςDCFΘ§
ΓύCE=CFΘ§ΓœBCE=ΓœDCFΘ§
ΓΏΓœGCE=45ΓψΘ§
ΓύΓœBCE+ΓœDCG=45ΓψΘ§
ΓύΓœDCF+ΓœDCG=45ΓψΘ§Φ¥ΓœGCF=45ΓψΘ§
ΓύΓœGCF=ΓœGCEΘ§
‘ΎΓςCEGΚΆΓςCFG÷–Θ§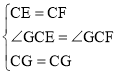 Θ§
Θ§
ΓύΓςCEGΓ’ΓςCFGΘ§
ΓύGE=GF=GD+DFΘ°
Θ®2Θ©Β±Π¬=2ΠΝ ±Θ§GE=GD+DF»‘»Μ≥…ΝΔΘ§άμ”…»γœ¬ΘΚ
»γΆΦΘ§―”≥ΛADΒΫFΘ§ ΙDF=BEΘ§Ν§Ϋ”CFΘ§
‘ΎΓςBCEΚΆΓςDCF÷–Θ§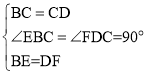 Θ§
Θ§
ΓύΓςBCEΓ’ΓςDCFΘ§
ΓύCE=CFΘ§ΓœBCE=ΓœDCFΘ§
ÿEG=GD+BEȧ
ΓύEG=GD+DF=GFΘ§
‘ΎΓςCEGΚΆΓςCFG÷–Θ§ Θ§
Θ§
ΓύΓςCEGΓ’ΓςCFGΘ§
ΓύΓœECG=ΓœFCGΘ§
ΓύΓœECG=ΓœDCF+ΓœDCG=ΓœBCE+ΓœDCGΘ§
ΓύΓœBCD=2ΓœECGΘ§Φ¥Π¬=2ΠΝΘ§
ΓύΒ±Π¬=2ΠΝ ±Θ§ΆΦ1÷–GEΘ§BEΘ§GD»ΐœΏΕΈ÷°ΦδΒΡΙΊœΒ»‘»Μ≥…ΝΔΘ°
Θ®3Θ©»γΆΦΘ§―”≥ΛBAΘ§ΫΜy÷α”ΎHΘ§
ΓΏΫΪ’ΐΖΫ–ΈOABC»ΤOΒψΥ≥ ±’κ–ΐΉΣΘ§
ΓύΓœHOA=ΓœNOCΘ§
‘ΎΓςHOAΚΆΓςNOC÷–Θ§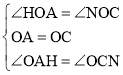 Θ§
Θ§
ΓύΓςHOAΓ’ΓςNOCΘ§
ΓύAH=CNΘ§OH=ONΘ§
ΓΏ÷±œΏOMΒΡΫβΈω ΫΈΣy=xΘ§
ΓύΓœHOM=ΓœMON=45ΓψΘ§
‘ΎΓςHOMΚΆΓςNOM÷–Θ§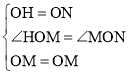 Θ§
Θ§
ΓύHM=MNΘ§
ΓύMN=AM+AH=AM+CNΘ§
ΓύΓςBMNΒΡ÷ή≥Λp=BM+MN+BN=BM+AM+CN+BN=AB+BC=2Θ§
ΓύΓςBMNΒΡ÷ή≥ΛΟΜ”–±δΜ·Θ§÷ή≥ΛΈΣ2Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
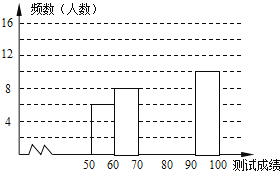
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΈΣΝΥΝΥΫβΤΏΡξΦΕ―ß…ζΧε”ΐ≤β ‘≥…Φ®«ιΩωΘ§œ÷¥”÷–ΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΒΡΧε”ΐ≥…Φ®Ά≥ΦΤ»γœ¬Θ§Τδ÷–”“≤ύ…»–ΈΆ≥ΦΤΆΦ÷–ΒΡ‘≤–ΡΫ«ΠΝΈΣ36ΓψΘ§ΗυΨίΆΦ±μ÷–ΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Χε”ΐ≥…Φ®Ά≥ΦΤ±μ | ||
Χε”ΐ≥…Φ®Θ®Ζ÷Θ© | »Υ ΐΘ®»ΥΘ© | ΑΌΖ÷±»Θ®%Θ© |
26 | 8 | 16 |
27 | 12 | 24 |
28 | 15 | |
29 | n | |
30 | ||
Θ®1Θ©«σ―υ±Ψ»ίΝΩΦΑnΒΡ÷ΒΘΜ
Θ®2Θ©“―÷ΣΗΟ–ΘΤΏΡξΦΕΙ≤”–500Οϊ―ß…ζΘ§»γΙϊΧε”ΐ≥…Φ®¥ο28Ζ÷“‘…œΈΣ”≈–ψΘ§«κΙάΦΤΗΟ–ΘΤΏΡξΦΕ―ß…ζΧε”ΐ≥…Φ®¥οΒΫ”≈–ψΒΡΉή»Υ ΐΘ°

ΓΨΧβΡΩΓΩΓΑ…Ά÷–ΜΣ Ϊ¥ Θ§―ΑΈΡΜ·Μυ“ρΘ§ΤΖ…ζΜν÷°ΟάΓ±Θ§Ρ≥–ΘΨΌΑλΝΥ ΉΫλΓΑ÷–Ιζ Ϊ¥ ¥σΜαΓ±Θ§Ψ≠―ΓΑΈΚσ”–50Οϊ―ß…ζ≤ΈΦ”Ψω»ϋΘ§’β50Οϊ―ß…ζΆ§ ±Ρ§–¥50 ΉΙ≈ Ϊ¥ Θ§»τΟΩ’ΐ»ΖΡ§–¥≥ω“Μ ΉΙ≈ Ϊ¥ ΒΟ2Ζ÷Θ§ΗυΨί≤β ‘≥…Φ®Μφ÷Τ≥ω≤ΩΖ÷ΤΒ ΐΖ÷≤Φ±μΚΆ≤ΩΖ÷ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ»γΆΦ±μΘΚ
Ήι±π | ≥…Φ®xΖ÷ | ΤΒ ΐ |
ΒΎ1Ήι |
| 6 |
ΒΎ2Ήι |
| 8 |
ΒΎ3Ήι |
| 14 |
ΒΎ4Ήι |
| a |
ΒΎ5Ήι |
| 10 |
«κΫαΚœΆΦ±μΆξ≥…œ¬Ν–ΗςΧβΘΚ
![]() «σ±μ÷–aΒΡ÷ΒΘΜ
«σ±μ÷–aΒΡ÷ΒΘΜ ![]() ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ≤Ι≥δΆξ’ϊΘΜ
ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ≤Ι≥δΆξ’ϊΘΜ
![]() »τ≤β ‘≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΈΣ”≈–ψΘ§‘ρ±Ψ¥Έ≤β ‘ΒΡ”≈–ψ¬ «Εύ…ΌΘΩ
»τ≤β ‘≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΈΣ”≈–ψΘ§‘ρ±Ψ¥Έ≤β ‘ΒΡ”≈–ψ¬ «Εύ…ΌΘΩ
![]() ΒΎ5Ήι10ΟϊΆ§―ß÷–Θ§”–4ΟϊΡ–Ά§―ßΘ§œ÷ΫΪ’β10ΟϊΆ§―ßΤΫΨυΖ÷≥…ΝΫΉιΫχ––Ε‘ΩΙΝΖœΑΘ§«“4ΟϊΡ–Ά§―ßΟΩΉιΖ÷ΝΫ»ΥΘ§«σ–ΓΟς”κ–Γ«ΩΝΫΟϊΡ–Ά§―ßΡήΖ÷‘ΎΆ§“ΜΉιΒΡΗ≈¬ Θ°
ΒΎ5Ήι10ΟϊΆ§―ß÷–Θ§”–4ΟϊΡ–Ά§―ßΘ§œ÷ΫΪ’β10ΟϊΆ§―ßΤΫΨυΖ÷≥…ΝΫΉιΫχ––Ε‘ΩΙΝΖœΑΘ§«“4ΟϊΡ–Ά§―ßΟΩΉιΖ÷ΝΫ»ΥΘ§«σ–ΓΟς”κ–Γ«ΩΝΫΟϊΡ–Ά§―ßΡήΖ÷‘ΎΆ§“ΜΉιΒΡΗ≈¬ Θ°