题目内容
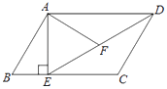
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.

【答案】见解析
【解析】试题分析:(1)根据矩形的得出OB=OA,∠ABC=∠BAD=90°,求出∠EBA=45°,可得AB=AE;求出∠OBA=60°,得出等边△OBA,推出BA=OA,从而AO=AE;
(2)由△OBA是等边三角形得∠BAO=60°,从而∠OAE=30°,然后根据等腰三角形的性质可求出∠AEO的度数,进而可求出∠FEO的度数.
解:∵四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,OB=OA,
∵BE平分∠ABC,
∴∠ABE=45°,
∵∠OBF=15°,
∴∠OBA=60°,
∵OB=OA,
∴△BOA是等边三角形,
∴∠OAB=60°,BA=OA,
∴∠OEF=∠BEA=180°-∠OAB-∠EBA=180°-45°-60°=75°,
∵∠BAF=90°,∠FBA=45°,
∴∠FBA=45°=∠BFA,
∴BA=AE,
∴AO=AE;
(2)∵∠BAD=90°,∠OAB=60°,
∴∠OAF=90°-60°=30°,
∴∠AEO=![]() ×(180°-30°)=75°,
×(180°-30°)=75°,
∴∠AOF=∠OEF=75°,
∴∠FEO=75°-45°=30°.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目