Question

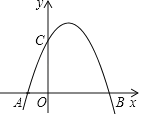
【题目】已知抛物线（是常数）经过点.

（1）求该抛物线的解析式和顶点坐标.

（2）若点在抛物线上，且点关于原点的对称点为.

①当点落在该抛物线上时，求的值；

②当点落在第二象限内，取得最小值时，求的值.

Answer 1

【答案】（1），顶点的坐标为(1,-4);（2）①，;②.

【解析】

（1）把坐标代入求出解析式，再化为顶点式即可求解；

（2）①由对称性可表示出P’的坐标，再由P和P’都在抛物线上，可得到m的方程，即可求出m的值；

②由点P’在第二象限，可求出t的取值，利用两点间的距离公式可用t表示，再由带你P’在抛物线上，可消去m，整理得到关于t的二次函数，利用二次函数的性质即可求出最小值时t的值，则可求出m的值.

（1）∵抛物线经过点，

∴，解得，∴抛物线的解析式为.

∵，∴顶点的坐标为.

（2）①由点在抛物线上，有.

∵关于原点的对称点为，有.

∴，即，

∴，

解得，.

②由题意知在第二象限，∴，，即，.

则在第四象限.

∵抛物线的顶点坐标为，∴.

过点作轴，为垂足，则.

∵，，

∴，.

当点和不重合时，在中，.

当点和重合时，，，符合上式.

∴，即.

记，则，

∴当时，取得最小值.

把代入，得，

解得，，

由，可知不符合题意，∴.