题目内容
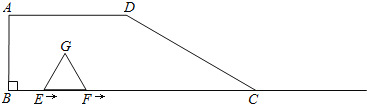
【题目】如图，在梯形ABCD中，AD∥BC，∠B=90°，BC=6，AD=3，∠DCB=30°．点E、F同时从B点出发，沿射线BC向右匀速移动，已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG，设E点移动距离为x（x＞0）．
（1）△EFG的边长是 （用含有x的代数式表示），当x=2时，点G的位置在 ；
（2）若△EFG与梯形ABCD重叠部分面积是y，求y与x之间的函数关系式；
（3）探究（2）中得到的函数y在x取何值时，存在最大值？并求出最大值．
【答案】（1）x，D点；（2）y=
x2；（3）当x=
时，y最大=
．
【解析】
试题分析：（1）根据等边三角形的三边相等，则△EFG的边长是点E移动的距离；根据等边三角形的三线合一和F点移动速度是E点移动速度的2倍，即可分析出BF=4，此时等边三角形的边长是2，则点G和点D重合；
（2）①当0＜x≤2时，重叠部分的面积即为等边三角形的面积；
②当2＜x≤6时，分两种情况：当2＜x＜3时和当3≤x≤6时，进行计算；
（3）分别求得（2）中每一种情况的最大值，再进一步比较取其中的最大值即可．
解：（1）∵点E、F同时从B点出发，沿射线BC向右匀速移动，且F点移动速度是E点移动速度的2倍，
∴BF=2BE=2x，
∴EF=BF﹣BE=2x﹣x=x，
∴△EFG的边长是x；
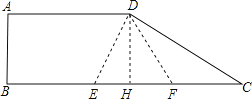
过D作DH⊥BC于H，得矩形ABHD及直角△CDH，连接DE、DF．
在直角△CDH中，∵∠C=30°，CH=BC﹣AD=3，
∴DH=CHtan30°=3×
当x=2时，BE=EF=2，
∵△EFG是等边三角形，且DH⊥BC交点H，
∴EH=HF=1
∴DE=DF=
=2，
∴△DEF是等边三角形，
∴点G的位置在D点．
故答案为x，D点；
（2）①当0＜x≤2时，△EFG在梯形ABCD内部，所以y=x2；
②分两种情况：
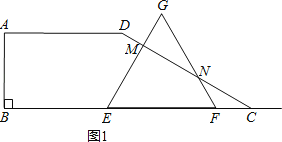
Ⅰ．当2＜x＜3时，如图1，点E、点F在线段BC上，
△EFG与梯形ABCD重叠部分为四边形EFNM，
∵∠FNC=∠FCN=30°，∴FN=FC=6﹣2x．∴GN=3x﹣6．
∵在Rt△NMG中，∠G=60°，GN=3x﹣6，
∴GM=
（3x﹣6），
由勾股定理得：MN=
（3x﹣6），
∴S△GMN=×GM×MN=×（3x﹣6）×（3x﹣6）=
（3x﹣6）2，
所以，此时y=
x2﹣（3x﹣6）2=﹣
；
Ⅱ．当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，
△EFG与梯形ABCD重叠部分为△ECP，
∵EC=6﹣x，
∴y=（6﹣x）2=x2﹣
x+
，
（3）当0＜x≤2时，
∵y=
x2，在x＞0时，y随x增大而增大，
∴x=2时，y最大=
；
当2＜x＜3时，∵y=﹣
在x=
时，y最大=
；
当3≤x≤6时，∵y=
，在x＜6时，y随x增大而减小，
∴x=3时，y最大=
．
综上所述：当x=时，y最大=．
