题目内容
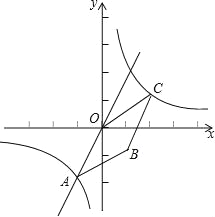
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
【答案】(1)反比例函数的解析式为y=![]() ;(2)-1<x<0或x>1;(3)四边形OABC是菱形.证明见解析.
;(2)-1<x<0或x>1;(3)四边形OABC是菱形.证明见解析.
【解析】
试题分析:(1)设反比例函数的解析式为y=![]() (k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;
(k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;
(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)首先求出OA的长度,结合题意CB∥OA且CB=![]() ,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
试题解析:(1)设反比例函数的解析式为y=![]() (k>0),
(k>0),
∵A(m,-2)在y=2x上,
∴-2=2m,
∴m=-1,
∴A(-1,-2),
又∵点A在y=![]() 上,
上,
∴k=2,
∴反比例函数的解析式为y=![]() ;
;
(2)观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为-1<x<0或x>1;
(3)四边形OABC是菱形.
证明:∵A(-1,-2),
∴OA=![]() ,
,
由题意知:CB∥OA且CB=![]() ,
,
∴CB=OA,
∴四边形OABC是平行四边形,
∵C(2,n)在y=![]() 上,
上,
∴n=1,
∴C(2,1),
OC=![]() ,
,
∴OC=OA,
∴四边形OABC是菱形.

【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是50 B.众数是51
C.方差是42 D.极差是21