Question

【题目】如图，在平面直角坐标系中，点A是反比例函数y=（k≠0）图象上一点，AB⊥x轴于B点，一次函数y=ax+b（a≠0）的图象交y轴于D（0，－2），交x轴于C点，并与反比例函数的图象交于A，E两点，连接OA，若△AOD的面积为4，且点C为OB中点．

（1）分别求双曲线及直线AE的解析式；

（2）若点Q在双曲线上，且S△QAB=4S△BAC，求点Q的坐标.

Answer 1

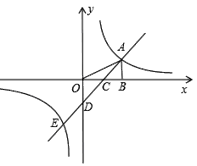
【答案】（1）y=x－2；（2）Q点的坐标为（12， ）或（－4，－2）．

【解析】试题分析：（1）先根据点D的坐标和△AOD的面积，求得点C的坐标，再结合点C为OB中点，求得点A的坐标，最后运用待定系数法求得反比例函数和一次函数的解析式；

（2）先设Q的坐标为（t， ），根据条件S△QAB=4S△BAC求得t的值，进而得到点Q的坐标．

试题解析：（1）∵D（0，-2），△AOD的面积为4，

∴×2×OB=4，

∴OB=4，

∵C为OB的中点，

∴OC=BC=2，C（2，0）

又∵∠COD=90°

∴△OCD为等腰直角三角形，

∴∠OCD=∠ACB=45°，

又∵AB⊥x轴于B点，

∴△ACB为等腰直角三角形，

∴AB=BC=2，

∴A点坐标为（4，2），

把A（4，2）代入y=，得k=4×2=8，

即反比例函数解析式为y=，

将C（2，0）和D（0，-2）代入一次函数y=ax+b，可得

，解得，

∴直线AE解析式为：y=x-2；

（2）设Q的坐标为（t， ），

∵S△BAC=×2×2=2，

∴S△QAB=4S△BAC=8，

即×2×|t-4|=8，

解得t=12或-4，

在y=中，当x=12时，y=；当x=-4时，y=-2，

∴Q点的坐标为（12， ）或（-4，-2）．