Question

平面内有四个点A、O、B、C，其中∠AOB=120⁰，∠ACB=60⁰，AO=BO=2，则满足题意的OC长度为整数的值可以是       ．

Answer 1

2，3，4

试题分析：考虑到∠AOB=120⁰，∠ACB=60⁰，AO=BO=2，分两种情况探究：
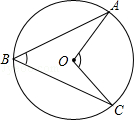
情况1，如图1，作△AOB，使∠AOB=120⁰， AO=BO=2，以点O 为圆心， 2为半径画圆，当点C在优弧AB上时，根据同弧所圆周角是圆心角一半，总有∠ACB=∠AOB=60⁰，此时，OC= AO=BO=2。

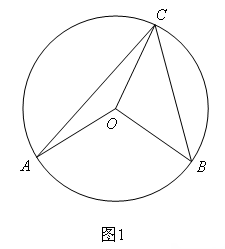
情况2，如图2，作菱形AOMB，使∠AOB=120⁰， AO=BO=AM=BM=2，以点M为圆心， 2为半径画圆，当点C在优弧AB上时，根据圆内接四边形对角互补，总有∠ACB=180⁰－∠AOB=60⁰。此时，OC的最大值是OC为⊙M的直径4时，所以，2＜OC≤4，整数有3，4。

综上所述，满足题意的OC长度为整数的值可以是2，3，4。