Question

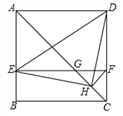
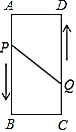
【题目】如图，长方形中，，，动点、分别从点、同时出发，点以2厘米/秒的速度向终点移动，点以1厘米/秒的速度向移动，当有一点到达终点时，另一点也停止运动．设运动的时间为秒，当________时，以点、、为顶点的三角形是等腰三角形．

Answer 1

【答案】或或或

【解析】

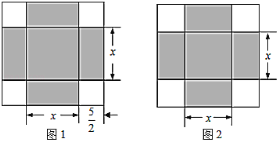
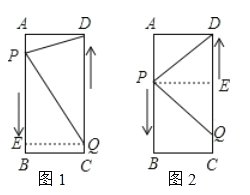
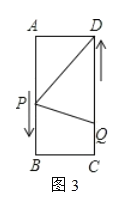
分情况讨论，如图1，当PQ＝DQ时，如图2，当PD＝PQ时，如图3，当PD＝QD时，由等腰三角形的性质及勾股定理建立方程就可以得出结论．

解：如图1，当PQ＝DQ时，作QE⊥AB于E，

∴∠PEQ＝90°，

∵∠B＝∠C＝90°，

∴四边形BCQE是矩形，

∴QE＝BC＝2cm，BE＝CQ＝t．

∵AP＝2t，

∴PE＝6﹣2t﹣t＝6﹣3t．DQ＝6﹣t．

∵PQ＝DQ，

∴PQ＝6﹣t．

在RtPQE中，由勾股定理，得

（6﹣3t）2+4＝（6﹣t）2，

解得：t＝．

如图2，当PD＝PQ时，

作PE⊥DQ于E，

∴DE＝QE＝DQ，∠PED＝90°．

∵∠B＝∠C＝90°，

∴四边形BCQE是矩形，

∴PE＝BC＝2cm．

∵DQ＝6﹣t，

∴DE＝．

∴2t＝，

解得：t＝；

如图5，当PD＝QD时，

∵AP＝2t，CQ＝t，

∴DQ＝6﹣t，

∴PD＝6﹣t．

在RtAPD中，由勾股定理，得

4+4t2＝（6﹣t）2，

解得t1＝，t2＝（舍去）．

综上所述：t＝，，，．

故答案为：，，，．