ΧβΡΩΡΎ»ί
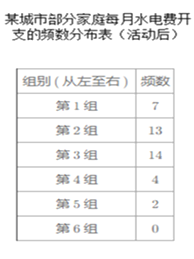
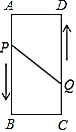
ΓΨΧβΡΩΓΩ»γΆΦΘ§±Ώ≥ΛΈΣ6ΒΡΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§D «AB±Ώ…œΒΡ“ΜΕ·ΒψΘ§”…AœρB‘ΥΕ·(AΓΔB≤Μ÷ΊΚœ)Θ§F «BC―”≥ΛœΏ…œΒΡ“ΜΕ·ΒψΘ§”κDΆ§ ±“‘œύΆ§ΒΡΥΌΕ»”…CœρBC―”≥ΛœΏΖΫœρ‘ΥΕ·(”κC≤Μ÷ΊΚœ)Θ§ΙΐΒψDΉςDEΓΆACΘ§Ν§Ϋ”DFΫΜAC”ΎGΘ°
(1)Β±ΒψD‘ΥΕ·ΒΫABΒΡ÷–Βψ ±Θ§÷±Ϋ”–¥≥ωAEΒΡ≥ΛΘ°
(2)Β±DFΓΆAB ±Θ§«σADΒΡ≥ΛΘ°
(3)‘Ύ‘ΥΕ·Ιΐ≥Χ÷–œΏΕΈGEΒΡ≥Λ «ΖώΖΔ…ζ±δΜ·ΘΩ»γΙϊ≤Μ±δΘ§«σ≥ωœΏΕΈGEΒΡ≥ΛΘΚ»γΙϊΖΔ…ζΗΡ±δ«κΥΒΟςάμ”…Θ°

ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®2Θ©2 Θ®3Θ©≤Μ±δΘΜ3
Θ®2Θ©2 Θ®3Θ©≤Μ±δΘΜ3
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΒψD‘ΥΕ·ΒΫABΒΡ÷–ΒψΒΟΒΫADΘΫ![]() ABΘΫ3Θ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟΘΚΓœAΘΫ60ΓψΘ§«σΒΟΓœADEΘΫ30ΓψΘ§ΗυΨί÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
ABΘΫ3Θ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟΘΚΓœAΘΫ60ΓψΘ§«σΒΟΓœADEΘΫ30ΓψΘ§ΗυΨί÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©”…ΒψEΓΔFΆ§ ±‘ΥΕ·«“ΥΌΕ»œύΆ§ΒΟΒΫADΘΫCFΘ§«σ≥ωΓœAGDΘΫΓœCGFΘΫ30ΓψΘ§ΓœFΘΫ30ΓψΘ§ΫχΕχΒΟΒΫCFΘΫCGΘΫADΘ§…ηADΘΫCGΘΫCFΘΫxΘ§‘ρAGΘΫ2xΘ§Ν–ΖΫ≥ΧΦ¥Ω…«σΫβΘΜ
Θ®3Θ©ΉςFQΓΆACΘ§ΫΜœΏΕΈACΒΡ―”≥ΛœΏ”ΎΒψQΘ§Ν§Ϋ”FEΘ§DQΘ§“Ή÷ΣADΘΫCFΘ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœAΘΫΓœABCΘΫΓœQCFΘΫ60ΓψΘ§ΦΧΕχΆΤ≥ωΓςADEΓ’ΓςCFQ(AAS)Θ§”…AEΘΫCQΘ§DEΘΫQF«“DEΓΈQFΩ…ΒΟΥΡ±Ώ–ΈDEFQ «ΤΫ––ΥΡ±Ώ–ΈΘ§ΦΧΕχΩ…÷Σ GEΘΫ![]() EQΘ§ΆΤ≥ωGEΘΫ
EQΘ§ΆΤ≥ωGEΘΫ![]() ACΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
ACΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
ΫβΘΚ(1)ΒψD‘ΥΕ·ΒΫABΒΡ÷–Βψ ±Θ§
ΓΏADΘΫ![]() ABΘΫ3Θ§ΓœAΘΫ60ΓψΘ§
ABΘΫ3Θ§ΓœAΘΫ60ΓψΘ§
ÿDEâACȧ
ΓύΓœADEΘΫ30ΓψΘ§
ΓύAEΘΫ![]() ADΘΫ
ADΘΫ![]() ΘΜ
ΘΜ
(2)ΓΏΒψDΓΔFΆ§ ±‘ΥΕ·«“ΥΌΕ»œύΆ§Θ§
ΓύADΘΫCFΘ§
ΓΏDFΓΆABΘ§ΓœAΘΫ60ΓψΘ§
ΓύΓœAGDΘΫΓœCGFΘΫ30ΓψΘ§
ΓΏΓœBΘΫ60ΓψΘ§
ΓύΓœFΘΫ30ΓψΘ§
ΓύΓœCGFΘΫΓœFΘ§
ΓύCFΘΫCGΘΫADΘ§
…ηADΘΫCGΘΫCFΘΫxΘ§‘ρAGΘΫ2xΘ§
ΓύAG+CGΘΫ2x+xΘΫ3xΘΫ6Θ§
ΓύxΘΫ2Θ§
ΓύADΘΫ2ΘΜ
(3)Β±ΒψDΓΔFΆ§ ±‘ΥΕ·«“ΥΌΕ»œύΆ§ ±Θ§œΏΕΈGEΒΡ≥ΛΕ»≤ΜΜαΗΡ±δΘ°άμ”…»γœ¬ΘΚ
ΉςFQΓΆACΘ§ΫΜœΏΕΈACΒΡ―”≥ΛœΏ”ΎΒψQΘ§Ν§Ϋ”FEΘ§DQΘ§
”÷ΓΏDEΓΆAB”ΎEΘ§
ΓύΓœGQFΘΫΓœAEDΘΫ90ΓψΘ§
ΓΏΒψDΓΔFΥΌΕ»œύΆ§Θ§
ΓύADΘΫCFΘ§
ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœAΘΫΓœABCΘΫΓœQCFΘΫ60ΓψΘ§
‘ΎΓςADEΚΆΓςCFQ÷–Θ§
ΓΏΓœAEDΘΫΓœCQFΘΫ90ΓψΘ§
ΓύΓœAEDΘΫΓœCQFΘ§

‘ΎΓςADEΚΆΓςCQF÷–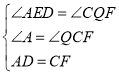 Θ§
Θ§
ΓύΓςADEΓ’ΓςCFQ(AAS)Θ§
ΓύAEΘΫCQΘ§DEΘΫQF«“DEΓΈQFΘ§
ΓύΥΡ±Ώ–ΈDEFQ «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύGEΘΫ![]() EQΘ§
EQȧ
ΓΏEC+AEΘΫCE+CQΘΫACΘ§
ΓύGEΘΫ![]() ACΘ§
ACȧ
”÷ΓΏΒ»±ΏΓςABCΒΡ±Ώ≥ΛΈΣ6Θ§
ΓύGEΘΫ3Θ§
ΓύΒψDΓΔFΆ§ ±‘ΥΕ·«“ΥΌΕ»œύΆ§ ±Θ§œΏΕΈGEΒΡ≥ΛΕ»≤ΜΜαΗΡ±δΘ°

 ÷–ΩΦΫβΕΝΩΦΒψΨΪΝΖœΒΝ–¥πΑΗ
÷–ΩΦΫβΕΝΩΦΒψΨΪΝΖœΒΝ–¥πΑΗ ΗςΒΊΤΎΡ©Η¥œΑΧΊ―ΒΨμœΒΝ–¥πΑΗ
ΗςΒΊΤΎΡ©Η¥œΑΧΊ―ΒΨμœΒΝ–¥πΑΗ